第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. [2024平顶山模拟]下列选项错误的是(
A. 平行四边形的对角线互相平分
B. 矩形的对角线相等
C. 对角线互相平分的四边形是平行四边形
D. 对角线相等的四边形是矩形
D
)A. 平行四边形的对角线互相平分
B. 矩形的对角线相等
C. 对角线互相平分的四边形是平行四边形
D. 对角线相等的四边形是矩形
答案:
D
2. 母题教材P19习题T2如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE= 3∠BAE,则∠CBD等于(

A. 22.5°
B. 30°
C. 45°
D. 60°
A
)
A. 22.5°
B. 30°
C. 45°
D. 60°
答案:
A
3. 如图,四边形ABCD是矩形,对角线AC,BD相交于点O,若DE垂直平分OC,且OC= 2,则DE的长度为(
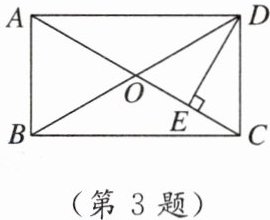
A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
C
)
A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
答案:
C
4. 情境题周末游玩某儿童乐园摩天轮的正面示意图如图所示,若每个舱看作一个点,任意选择四个点,则以这四个点为顶点的四边形是矩形的有(

A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
5. 如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF= 90°.
(1)求证:四边形ABDF是矩形;
(2)若AD= 5,DF= 3,求四边形ABCF的面积S.

(1)【证明】∵四边形ABCD是平行四边形,
∴BA//CD.
∴∠BAE=∠FDE.
∵点E是AD的中点,
∴AE=DE.
在△BEA和△FED中,
$\left\{ \begin{array} { l } { \angle B A E = \angle F D E, } \\ { A E = D E, } \\ { \angle B E A = \angle F E D, } \end{array} \right.$
∴△BEA≌△FED(ASA).
∴EF=EB.
又∵AE=DE,
∴四边形ABDF是平行四边形.
又∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)【解】由(1)得四边形ABDF是矩形,
∴∠AFD=90°,AB=DF=3,AF=BD,
∴AF=$\sqrt{AD^{2}-DF^{2}}$=$\sqrt{5^{2}-3^{2}}$=
∴S_{矩形ABDF}=DF·AF=3×4=
∵四边形ABCD是平行四边形,
∴CD=AB=3.
∵∠BDF=90°,∴∠BDC=90°.
∴$S_{△BCD}$=$\frac{1}{2}$BD·CD=$\frac{1}{2}$×4×3=
∴四边形ABCF的面积S=$S_{矩形ABDF}+S_{△BCD}$=12+6=
(1)求证:四边形ABDF是矩形;
(2)若AD= 5,DF= 3,求四边形ABCF的面积S.

(1)【证明】∵四边形ABCD是平行四边形,
∴BA//CD.
∴∠BAE=∠FDE.
∵点E是AD的中点,
∴AE=DE.
在△BEA和△FED中,
$\left\{ \begin{array} { l } { \angle B A E = \angle F D E, } \\ { A E = D E, } \\ { \angle B E A = \angle F E D, } \end{array} \right.$
∴△BEA≌△FED(ASA).
∴EF=EB.
又∵AE=DE,
∴四边形ABDF是平行四边形.
又∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)【解】由(1)得四边形ABDF是矩形,
∴∠AFD=90°,AB=DF=3,AF=BD,
∴AF=$\sqrt{AD^{2}-DF^{2}}$=$\sqrt{5^{2}-3^{2}}$=
4
.∴S_{矩形ABDF}=DF·AF=3×4=
12
,BD=AF=4.∵四边形ABCD是平行四边形,
∴CD=AB=3.
∵∠BDF=90°,∴∠BDC=90°.
∴$S_{△BCD}$=$\frac{1}{2}$BD·CD=$\frac{1}{2}$×4×3=
6
.∴四边形ABCF的面积S=$S_{矩形ABDF}+S_{△BCD}$=12+6=
18
.
答案:
(1)【证明】
∵四边形ABCD是平行四边形,
∴BA//CD.
∴∠BAE=∠FDE.
∵点E是AD的中点,
∴AE=DE.
在△BEA和△FED中,
$\left\{ \begin{array} { l } { \angle B A E = \angle F D E, } \\ { A E = D E, } \\ { \angle B E A = \angle F E D, } \end{array} \right.$
∴△BEA≌△FED(ASA).
∴EF=EB.
又
∵AE=DE,
∴四边形ABDF是平行四边形.
又
∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)【解】由
(1)得四边形ABDF是矩形,
∴∠AFD=90°,AB=DF=3,AF=BD,
∴AF=$\sqrt{AD^{2}-DF^{2}}$=$\sqrt{5^{2}-3^{2}}$=4.
∴S_{矩形ABDF}=DF·AF=3×4=12,BD=AF=4.
∵四边形ABCD是平行四边形,
∴CD=AB=3.
∵∠BDF=90°,
∴∠BDC=90°.
∴$S_{△BCD}$=$\frac{1}{2}$BD·CD=$\frac{1}{2}$×4×3=6.
∴四边形ABCF的面积S=$S_{矩形ABDF}+S_{△BCD}$=12+6=18.
(1)【证明】
∵四边形ABCD是平行四边形,
∴BA//CD.
∴∠BAE=∠FDE.
∵点E是AD的中点,
∴AE=DE.
在△BEA和△FED中,
$\left\{ \begin{array} { l } { \angle B A E = \angle F D E, } \\ { A E = D E, } \\ { \angle B E A = \angle F E D, } \end{array} \right.$
∴△BEA≌△FED(ASA).
∴EF=EB.
又
∵AE=DE,
∴四边形ABDF是平行四边形.
又
∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)【解】由
(1)得四边形ABDF是矩形,
∴∠AFD=90°,AB=DF=3,AF=BD,
∴AF=$\sqrt{AD^{2}-DF^{2}}$=$\sqrt{5^{2}-3^{2}}$=4.
∴S_{矩形ABDF}=DF·AF=3×4=12,BD=AF=4.
∵四边形ABCD是平行四边形,
∴CD=AB=3.
∵∠BDF=90°,
∴∠BDC=90°.
∴$S_{△BCD}$=$\frac{1}{2}$BD·CD=$\frac{1}{2}$×4×3=6.
∴四边形ABCF的面积S=$S_{矩形ABDF}+S_{△BCD}$=12+6=18.
6. [2023沧州期末]如图,在Rt△ABC中,∠ACB= 90°,BC= 8,AC= 6,P为边AB上一动点(P不与B,A重合),PE⊥AC于E,PF⊥BC于F,M为EF的中点,则CM的取值范围是(
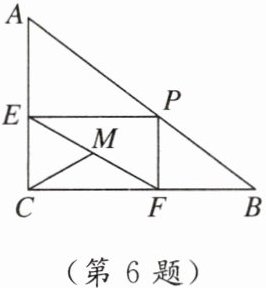
A. $\frac{12}{5}\leqslant CM<4$
B. $3\leqslant CM<\frac{24}{5}$
C. $\frac{12}{5}\leqslant CM<3$
D. $\frac{24}{5}\leqslant CM<6$
A
)
A. $\frac{12}{5}\leqslant CM<4$
B. $3\leqslant CM<\frac{24}{5}$
C. $\frac{12}{5}\leqslant CM<3$
D. $\frac{24}{5}\leqslant CM<6$
答案:
A
7. 如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG,若AF= 3,DG= 4,FG= 5,则矩形ABCD的面积为(

A. 12
B. 24
C. 36
D. 48
D
)
A. 12
B. 24
C. 36
D. 48
答案:
D
8. 新考法折叠法如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH= 6,EF= 8,下列结论:

①∠HEF= 90°;②△AEH≌△CGF;③AD= HF;④FE= 2AE;⑤AB= 9.6.
其中正确结论的个数是(
A. 2
B. 3
C. 4
D. 5

①∠HEF= 90°;②△AEH≌△CGF;③AD= HF;④FE= 2AE;⑤AB= 9.6.
其中正确结论的个数是(
4
)A. 2
B. 3
C. 4
D. 5
答案:
C 【点拨】
∵将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,
∴EA=EM,BE=EM,∠AEH=∠HEM,∠BEF=∠FEM,∠EMH=∠A=90°,∠C=90°.
∴AB=AE+EB=2EM.
∵∠AEH+∠HEM+∠BEF+∠FEM=180°,
∴∠HEF=∠HEM+∠FEM=$\frac{1}{2}$×180°=90°.故①正确;
同理,∠EFG=∠FGH=90°,
∴四边形EFGH是矩形.
∴EH=GF.
易知AB=2AE,CD=2CG,AB=CD,
∴AE=CG.
又
∵∠A=∠C=90°,
∴Rt△AEH≌Rt△CGF(HL).故②正确;
∴AH=CF.
由翻折可知,CF=NF,DH=HN,
∴AH=CF=NF.
∴AD=AH+DH=NF+HN=HF.故③正确;
∵EH=6,EF=8,
∴HF=$\sqrt{EH^{2}+EF^{2}}$=10.
∵EM·HF=EH·EF,
∴EM=$\frac{EH·EF}{HF}$=$\frac{6×8}{10}$=4.8.
∴AB=2×4.8=9.6.故⑤正确;
∵EF=8,2AE=AB=9.6,
∴EF≠2AE,故④错误.
综上所述,正确的结论是①②③⑤,共4个.
∵将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,
∴EA=EM,BE=EM,∠AEH=∠HEM,∠BEF=∠FEM,∠EMH=∠A=90°,∠C=90°.
∴AB=AE+EB=2EM.
∵∠AEH+∠HEM+∠BEF+∠FEM=180°,
∴∠HEF=∠HEM+∠FEM=$\frac{1}{2}$×180°=90°.故①正确;
同理,∠EFG=∠FGH=90°,
∴四边形EFGH是矩形.
∴EH=GF.
易知AB=2AE,CD=2CG,AB=CD,
∴AE=CG.
又
∵∠A=∠C=90°,
∴Rt△AEH≌Rt△CGF(HL).故②正确;
∴AH=CF.
由翻折可知,CF=NF,DH=HN,
∴AH=CF=NF.
∴AD=AH+DH=NF+HN=HF.故③正确;
∵EH=6,EF=8,
∴HF=$\sqrt{EH^{2}+EF^{2}}$=10.
∵EM·HF=EH·EF,
∴EM=$\frac{EH·EF}{HF}$=$\frac{6×8}{10}$=4.8.
∴AB=2×4.8=9.6.故⑤正确;
∵EF=8,2AE=AB=9.6,
∴EF≠2AE,故④错误.
综上所述,正确的结论是①②③⑤,共4个.
查看更多完整答案,请扫码查看


