《2025年综合应用创新题典中点九年级数学上册北师大版》

13. 如图,已知等腰三角形ABC的顶角$∠BAC$的大小为θ,点D为边BC上的动点(与B,C不重合),将AD绕点A沿顺时针方向旋转θ时点D落在$D'$处,连接$BD'$.给出下列结论:
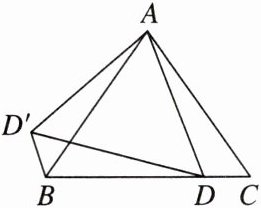
①$\triangle ACD\cong \triangle ABD'$;
②$\triangle ACB\backsim \triangle ADD'$;
③当$BD= CD$时,$\triangle ADD'$的面积取得最小值.
其中正确的结论有______①②③(填结论对应的序号).

答案： ①②③ 【点拨】由题意可知 $ AC = AB $，$ AD = AD' $， $ ∠DAD' = θ = ∠CAB $，$ ∴ ∠CAD = ∠BAD' $。 $ ∴ △ACD \cong △ABD' $，故①正确； $ \because AC = AB $，$ AD = AD' $， $ \therefore \frac{AC}{AB} = 1 = \frac{AD}{AD'} $。$ \therefore \frac{AC}{AD} = \frac{AB}{AD'} $。又 $ \because ∠BAC = ∠D'AD $， $ \therefore △ACB \backsim △ADD' $，故②正确； $ \because △ACB \backsim △ADD' $， $ \therefore \frac{S_{△ADD'}}{S_{△ACB}} = (\frac{AD}{AC})^2 $。 $ \because $ 当 $ AD ⊥ BC $ 时，$ AD $ 的值最小，$ ∴ $ 此时 $ △ADD' $ 的面积取得最小值。又 $ \because AB = AC $， $ \therefore BD = CD $。 $ \therefore $ 当 $ BD = CD $ 时，$ △ADD' $ 的面积取得最小值，故③正确。

14. [2024济南钢城区期末]如图,在四边形ABCD中,AC,BD是四边形ABCD的两条对角线,点E,F,G,H分别是在四边形ABCD的四边上的动点,但E,F,G,H不与A,B,C,D重合,且$EF// BD// GH$,$FG// AC// HE$.
(1)若对角线$AC= BD= a$(定值),求证:四边形EFGH的周长是定值;
(2)若$AC= m$,$BD= n$,$m,n$为定值,但$m≠n$,则四边形EFGH的周长是定值吗?请指出,并说明理由.

(1)证明：$ \because EF // BD // GH $，$ FG // AC // HE $， $ \therefore $ 四边形 $ EFGH $ 是平行四边形。 $ \therefore EH = GF $，$ EF = GH $。设 $ GH $ 为 $ x $，$ GF $ 为 $ y $，$ AH = p $，$ BH = q $。 $ \because GH // BD $， $ \therefore \frac{AH}{AB} = \frac{GH}{BD} $，即 $ \frac{p}{p + q} = \frac{x}{a} $。 $ \because HE // AC $， $ \therefore \frac{BH}{AB} = \frac{HE}{AC} $，即 $ \frac{q}{p + q} = \frac{y}{a} $。 $ \therefore x + y = \frac{a(p + q)}{p + q} = a $，故四边形 $ EFGH $ 的周长 $ = 2(x + y) = 2a $，是定值。(2)不是定值。理由：$ \because AC = m $，$ BD = n $， $ \therefore \frac{y}{m} = \frac{q}{p + q} $，$ \frac{x}{n} = \frac{p}{p + q} $， $ \therefore x + y = \frac{pn + qm}{p + q} = \frac{\frac{p}{q}n + m}{\frac{p}{q} + 1} $。 $ \because H $ 是 $ AB $ 上的动点，$ \therefore \frac{p}{q} $ 是变量。又 $ \because m $，$ n $ 为定值， $ \therefore x + y $ 随 $ \frac{p}{q} $ 的变化而变化。 $ \therefore x + y $ 不能确定，即四边形 $ EFGH $ 的周长不是定值。

答案： 【解】
(1)$ \because EF // BD // GH $，$ FG // AC // HE $， $ \therefore $ 四边形 $ EFGH $ 是平行四边形。 $ \therefore EH = GF $，$ EF = GH $。设 $ GH $ 为 $ x $，$ GF $ 为 $ y $，$ AH = p $，$ BH = q $。 $ \because GH // BD $， $ \therefore \frac{AH}{AB} = \frac{GH}{BD} $，即 $ \frac{p}{p + q} = \frac{x}{a} $。 $ \because HE // AC $， $ \therefore \frac{BH}{AB} = \frac{HE}{AC} $，即 $ \frac{q}{p + q} = \frac{y}{a} $。 $ \therefore x + y = \frac{a(p + q)}{p + q} = a $，故四边形 $ EFGH $ 的周长 $ = 2(x + y) = 2a $，是定值。
(2)不是定值。理由：$ \because AC = m $，$ BD = n $， $ \therefore \frac{y}{m} = \frac{q}{p + q} $，$ \frac{x}{n} = \frac{p}{p + q} $， $ \therefore x + y = \frac{pn + qm}{p + q} = \frac{\frac{p}{q}n + m}{\frac{p}{q} + 1} $。 $ \because H $ 是 $ AB $ 上的动点，$ \therefore \frac{p}{q} $ 是变量。又 $ \because m $，$ n $ 为定值， $ \therefore x + y $ 随 $ \frac{p}{q} $ 的变化而变化。 $ \therefore x + y $ 不能确定，即四边形 $ EFGH $ 的周长不是定值。

15. 新视角探究题探究:如图,$DE// BC$,$FG// AB$,$MN// AC$,且DE,FG,MN交于点P,若设$S_{\triangle DMP}= S_{1}$,$S_{\triangle PEF}= S_{2}$,$S_{\triangle GNP}= S_{3}$,$S_{\triangle ABC}= S$,$S与S_{1}$,$S_{2}$,$S_{3}$之间有什么结论?猜想并加以论证.
猜想：$\sqrt{S_1} + \sqrt{S_2} + \sqrt{S_3} = \sqrt{S}$。证明：$ \because MN // AC $，$ \therefore ∠DMP = ∠BAC $。 $ \because DE // BC $，$ \therefore ∠MDP = ∠ABC $。 $ \therefore △PDM \backsim △CBA $。 $ \therefore \frac{DM}{AB} = \frac{PD}{BC} $。 $ \because DE // BC $，$ FG // AB $， $ \therefore $ 四边形 $ DPG B $ 是平行四边形。 $ \therefore PD = BG $。 $ \therefore \frac{DM}{AB} = \frac{BG}{BC} $。同理 $ \frac{EF}{AC} = \frac{CN}{BC} $。 $ \therefore \frac{DM}{AB} + \frac{EF}{AC} + \frac{GN}{BC} = \frac{BG}{BC} + \frac{CN}{BC} + \frac{GN}{BC} = \frac{BC}{BC} = 1 $。由 $ △PDM \backsim △CBA $ 得 $ \frac{S_1}{S} = (\frac{DM}{AB})^2 $，即 $ \frac{\sqrt{S_1}}{\sqrt{S}} = \frac{DM}{AB} $，同理 $ \frac{\sqrt{S_2}}{\sqrt{S}} = \frac{EF}{AC} $，$ \frac{\sqrt{S_3}}{\sqrt{S}} = \frac{GN}{BC} $。 $ \therefore \frac{\sqrt{S_1}}{\sqrt{S}} + \frac{\sqrt{S_2}}{\sqrt{S}} + \frac{\sqrt{S_3}}{\sqrt{S}} = 1 $。 $ \therefore \sqrt{S_1} + \sqrt{S_2} + \sqrt{S_3} = \sqrt{S} $。

答案： 【解】猜想：$ \sqrt{S_1} + \sqrt{S_2} + \sqrt{S_3} = \sqrt{S} $。证明：$ \because MN // AC $，$ \therefore ∠DMP = ∠BAC $。 $ \because DE // BC $，$ \therefore ∠MDP = ∠ABC $。 $ \therefore △PDM \backsim △CBA $。 $ \therefore \frac{DM}{AB} = \frac{PD}{BC} $。 $ \because DE // BC $，$ FG // AB $， $ \therefore $ 四边形 $ DPG B $ 是平行四边形。 $ \therefore PD = BG $。 $ \therefore \frac{DM}{AB} = \frac{BG}{BC} $。同理 $ \frac{EF}{AC} = \frac{CN}{BC} $。 $ \therefore \frac{DM}{AB} + \frac{EF}{AC} + \frac{GN}{BC} = \frac{BG}{BC} + \frac{CN}{BC} + \frac{GN}{BC} = \frac{BC}{BC} = 1 $。由 $ △PDM \backsim △CBA $ 得 $ \frac{S_1}{S} = (\frac{DM}{AB})^2 $，即 $ \frac{\sqrt{S_1}}{\sqrt{S}} = \frac{DM}{AB} $，同理 $ \frac{\sqrt{S_2}}{\sqrt{S}} = \frac{EF}{AC} $，$ \frac{\sqrt{S_3}}{\sqrt{S}} = \frac{GN}{BC} $。 $ \therefore \frac{\sqrt{S_1}}{\sqrt{S}} + \frac{\sqrt{S_2}}{\sqrt{S}} + \frac{\sqrt{S_3}}{\sqrt{S}} = 1 $。 $ \therefore \sqrt{S_1} + \sqrt{S_2} + \sqrt{S_3} = \sqrt{S} $。