第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 下列四组图形中,一定相似的是(
A. 正方形与矩形
B. 正方形与菱形
C. 菱形与菱形
D. 正五边形与正五边形
D
)A. 正方形与矩形
B. 正方形与菱形
C. 菱形与菱形
D. 正五边形与正五边形
答案:
D [点拨]判定是否是相似多边形时,一定要同时从两个方面判定:对应角是否相等,对应边是否成比例,二者缺一不可.
2. 已知$\triangle ABC\backsim\triangle DEF$,$\frac{AB}{DE}= \frac{1}{2}$,若$BC = 2$,则$EF = $(
A. 4
B. 6
C. 8
D. 16
A
)A. 4
B. 6
C. 8
D. 16
答案:
A
3. 下列命题为假命题的是(
A. 任意两个等腰直角三角形相似
B. 有一个角为$36^{\circ}$的两个等腰三角形相似
C. 任意两个等边三角形相似
D. 有一个角为$20^{\circ}$的两个直角三角形相似
B
)A. 任意两个等腰直角三角形相似
B. 有一个角为$36^{\circ}$的两个等腰三角形相似
C. 任意两个等边三角形相似
D. 有一个角为$20^{\circ}$的两个直角三角形相似
答案:
B [点拨]A.任意两个等腰直角三角形相似,是真命题;
B.有一个角为36°的两个等腰三角形,没有指明36°是顶角还是底角,这两个三角形相似,是假命题;
C.任意两个等边三角形相似,是真命题;
D.有一个角为20°的两个直角三角形相似,是真命题.
故选B.
B.有一个角为36°的两个等腰三角形,没有指明36°是顶角还是底角,这两个三角形相似,是假命题;
C.任意两个等边三角形相似,是真命题;
D.有一个角为20°的两个直角三角形相似,是真命题.
故选B.
4. [2023陕西]如图,$DE是\triangle ABC$的中位线,点$F在DB$上,$DF = 2BF$.连接$EF$并延长,与$CB的延长线相交于点M$.若$BC = 6$,则线段$CM$的长为(
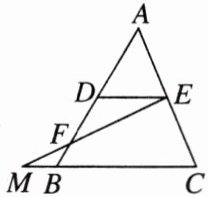

A. $\frac{13}{2}$
B. 7
C. $\frac{15}{2}$
D. 8
C
)

A. $\frac{13}{2}$
B. 7
C. $\frac{15}{2}$
D. 8
答案:
C [点拨]
∵DE是△ABC的中位线,
∴DE//BC,DE = $\frac{1}{2}$BC = 3.
易证△DEF∽△BMF,
∴$\frac{DE}{BM}$ = $\frac{DF}{BF}$ = $\frac{2BF}{BF}$ = 2.
∴BM = $\frac{3}{2}$.
∴CM = BC + BM = $\frac{15}{2}$.
故选C.
∵DE是△ABC的中位线,
∴DE//BC,DE = $\frac{1}{2}$BC = 3.
易证△DEF∽△BMF,
∴$\frac{DE}{BM}$ = $\frac{DF}{BF}$ = $\frac{2BF}{BF}$ = 2.
∴BM = $\frac{3}{2}$.
∴CM = BC + BM = $\frac{15}{2}$.
故选C.
5. 母题教材P95习题T2如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与$\triangle A_{1}B_{1}C_{1}$相似的是(

B
)

答案:
B [点拨]因为△$A_{1}B_{1}C_{1}$中有一个角是135°,四个选项中,只有选项B中的阴影三角形有一个角是135°,且这两个三角形中135°角的两边对应成比例,所以选项B符合题意.
6. $\triangle ABC$的三边长分别为2,3,4,另有一个与它相似的$\triangle DEF$,其最长边为12,则$\triangle DEF$的周长是(
A. 54
B. 36
C. 27
D. 21
C
)A. 54
B. 36
C. 27
D. 21
答案:
C [点拨]设△DEF的另两边长分别为x,y(x<y),
∵△ABC与△DEF相似,
∴$\frac{2}{x}$ = $\frac{3}{y}$ = $\frac{4}{12}$.
∴x = 6,y = 9.
∴△DEF的周长是6 + 9 + 12 = 27,故选C.
∵△ABC与△DEF相似,
∴$\frac{2}{x}$ = $\frac{3}{y}$ = $\frac{4}{12}$.
∴x = 6,y = 9.
∴△DEF的周长是6 + 9 + 12 = 27,故选C.
7. [2023邢台月考]在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,用直尺和圆规在边$AB上确定一点D$,使$\triangle ACD\backsim\triangle CBD$,根据作图痕迹判断,下列正确的是(
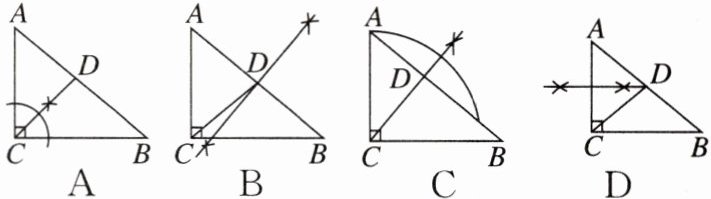
C
)
答案:
C [点拨]当CD是AB的垂线时,
∵CD⊥AB,
∴∠CDA = ∠BDC = 90°.
∴∠A + ∠ACD = 90° = ∠ACD + ∠BCD,
∴∠A = ∠BCD.
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的平分线,CD不一定与AB垂直,不符合题意;
B选项中,CD是△ABC的中线,CD不一定与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不一定与AB垂直,不符合题意.
故选C.
∵CD⊥AB,
∴∠CDA = ∠BDC = 90°.
∴∠A + ∠ACD = 90° = ∠ACD + ∠BCD,
∴∠A = ∠BCD.
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的平分线,CD不一定与AB垂直,不符合题意;
B选项中,CD是△ABC的中线,CD不一定与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不一定与AB垂直,不符合题意.
故选C.
8. 如图,点$E在矩形ABCD的AB$边上,将$\triangle ADE沿DE$翻折,点$A恰好落在BC边上的点F$处,若$CD = 3BF$,$BE = 4$,则$AD$的长为(

A. 9
B. 12
C. 15
D. 18
C
)
A. 9
B. 12
C. 15
D. 18
答案:
C [点拨]先证明△BEF∽△CFD,求得CF = 12,再设BF = x,用含有x的式子表示DF,CD,由勾股定理列出方程即可求解.
9. [2023临沂]如图,三角形纸片$ABC$中,$AC = 6$,$BC = 9$,分别沿与$BC$,$AC$平行的方向,从靠近$A的AB$边的三等分点剪去两个角,得到的平行四边形纸片的周长是______.
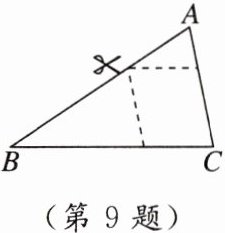

答案:
14 [点拨]如图,由题意得$\frac{AD}{AB}$ = $\frac{1}{3}$,四边形DECF是平行四边形,DF//BC,DE//AC.
∴$\frac{BD}{AB}$ = $\frac{2}{3}$,易得△ADF∽△ABC,△BDE∽△BAC;
∴$\frac{DF}{BC}$ = $\frac{AD}{AB}$ = $\frac{1}{3}$,$\frac{DE}{AC}$ = $\frac{BD}{AB}$ = $\frac{2}{3}$.
∵AC = 6,BC = 9,
∴DF = 3,DE = 4.
∴平行四边形纸片DECF的周长是2×(3 + 4) = 14.

14 [点拨]如图,由题意得$\frac{AD}{AB}$ = $\frac{1}{3}$,四边形DECF是平行四边形,DF//BC,DE//AC.
∴$\frac{BD}{AB}$ = $\frac{2}{3}$,易得△ADF∽△ABC,△BDE∽△BAC;
∴$\frac{DF}{BC}$ = $\frac{AD}{AB}$ = $\frac{1}{3}$,$\frac{DE}{AC}$ = $\frac{BD}{AB}$ = $\frac{2}{3}$.
∵AC = 6,BC = 9,
∴DF = 3,DE = 4.
∴平行四边形纸片DECF的周长是2×(3 + 4) = 14.

10. [2024泉州五中模拟]如图,$\triangle ABC$中,$AB = AC$,$\angle B = 72^{\circ}$,$\angle ACB的平分线CD交AB于点D$,则点$D是线段AB$的黄金分割点.若$AC = 2$,则$BD = $
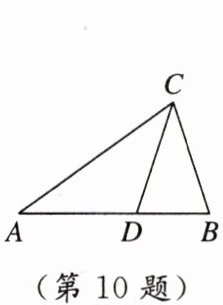
3 - $\sqrt{5}$
.
答案:
3 - $\sqrt{5}$
11. 新趋势·跨学科如图,一束光线从点$A(-2,5)$出发,经过$y轴上的点B(0,1)反射后经过点C(m,n)$,则$2m - n$的值是______.


答案:
-1 [点拨]如图,过点A作AG⊥y轴,过点C作CF⊥y轴,垂足分别为G,F,则∠AGB = ∠CFB = 90°.
由题意易知∠ABG = ∠CBF,
∴△AGB∽△CFB.
∴$\frac{BF}{BG}$ = $\frac{CF}{AG}$.
∴$\frac{BF}{CF}$ = $\frac{BG}{AG}$.
∵A(-2, 5),B(0, 1),C(m, n),
∴AG = 2,BG = 5 - 1 = 4,CF = -m,BF = 1 - n.
∴$\frac{BF}{CF}$ = $\frac{BG}{AG}$ = 2.
∴$\frac{BF}{CF}$ = $\frac{1 - n}{-m}$ = 2.
∴2m - n = -1.

-1 [点拨]如图,过点A作AG⊥y轴,过点C作CF⊥y轴,垂足分别为G,F,则∠AGB = ∠CFB = 90°.
由题意易知∠ABG = ∠CBF,
∴△AGB∽△CFB.
∴$\frac{BF}{BG}$ = $\frac{CF}{AG}$.
∴$\frac{BF}{CF}$ = $\frac{BG}{AG}$.
∵A(-2, 5),B(0, 1),C(m, n),
∴AG = 2,BG = 5 - 1 = 4,CF = -m,BF = 1 - n.
∴$\frac{BF}{CF}$ = $\frac{BG}{AG}$ = 2.
∴$\frac{BF}{CF}$ = $\frac{1 - n}{-m}$ = 2.
∴2m - n = -1.

12. [2023常德]如图①,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 8$,$BC = 6$,$D是AB$上一点,且$AD = 2$,过点$D作DE// BC交AC于E$,将$\triangle ADE绕A$点顺时针旋转到图②的位置,则图②中$\frac{BD}{CE}$的值为______

$\frac{4}{5}$
.
答案:
$\frac{4}{5}$ [点拨]在题图①中,
∵∠ABC = 90°,AB = 8,
BC = 6,
∴AC = $\sqrt{AB^{2} + BC^{2}}$ = $\sqrt{8^{2} + 6^{2}}$ = 10.
∵DE//BC,
∴∠ADE = ∠ABC,∠AED = ∠ACB.
∴△ADE∽△ABC.
∴$\frac{AD}{AB}$ = $\frac{AE}{AC}$.
∴$\frac{AD}{AE}$ = $\frac{AB}{AC}$.
在题图②中,由旋转的性质可得∠DAB = ∠EAC,且$\frac{AD}{AE}$ = $\frac{AB}{AC}$仍成立,
∴△ADB∽△AEC;
∴$\frac{BD}{EC}$ = $\frac{AB}{AC}$ = $\frac{8}{10}$ = $\frac{4}{5}$.
∵∠ABC = 90°,AB = 8,
BC = 6,
∴AC = $\sqrt{AB^{2} + BC^{2}}$ = $\sqrt{8^{2} + 6^{2}}$ = 10.
∵DE//BC,
∴∠ADE = ∠ABC,∠AED = ∠ACB.
∴△ADE∽△ABC.
∴$\frac{AD}{AB}$ = $\frac{AE}{AC}$.
∴$\frac{AD}{AE}$ = $\frac{AB}{AC}$.
在题图②中,由旋转的性质可得∠DAB = ∠EAC,且$\frac{AD}{AE}$ = $\frac{AB}{AC}$仍成立,
∴△ADB∽△AEC;
∴$\frac{BD}{EC}$ = $\frac{AB}{AC}$ = $\frac{8}{10}$ = $\frac{4}{5}$.
查看更多完整答案,请扫码查看


