第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 在平行四边形、矩形、菱形、正方形中,既是轴对称图形又是中心对称图形的有(
A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
2. 情境题 地域文化 粤绣凝聚着历代艺人的天才与智慧,从艺术风格到创作思维都充满了岭南特色.在“针尖上的画意——广绣精品与岭南绘画展”中,师傅要检验一个四边形画框是否为矩形,可行的测量方法是(
A. 测量四边形画框的两个角是否为$90^{\circ }$
B. 测量四边形画框的对角线是否相等且互相平分
C. 测量四边形画框的一组对边是否平行且相等
D. 测量四边形画框的四边是否相等
B
)
A. 测量四边形画框的两个角是否为$90^{\circ }$
B. 测量四边形画框的对角线是否相等且互相平分
C. 测量四边形画框的一组对边是否平行且相等
D. 测量四边形画框的四边是否相等
答案:
B
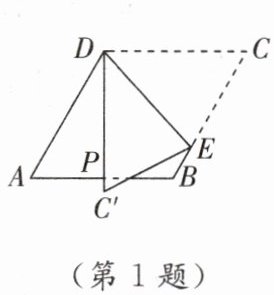
3. 如图,矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点,若$∠ACB= 30^{\circ },AB= 8$,则MN的长为(

A. 2
B. 4
C. 8
D. 16
B
)
A. 2
B. 4
C. 8
D. 16
答案:
B [点拨]根据矩形的性质和含30°角的直角三角形的性质得出AC = BD = 16,进而求出BO,再依据中位线的性质得MN = $\frac{1}{2}$BO。
4. 如图,在菱形ABCD中,AC,BD交于点O,$AC= 8,BD= 6$,点P为线段AC上的一个动点,过点P分别作$PM⊥AD$于点M,$PN⊥DC$于点N,则$PM+PN$的值为(

A. $\frac {48}{5}$
B. $\frac {1}{5}$
C. $\frac {24}{5}$
D. $\frac {2}{3}$
C
)
A. $\frac {48}{5}$
B. $\frac {1}{5}$
C. $\frac {24}{5}$
D. $\frac {2}{3}$
答案:
C
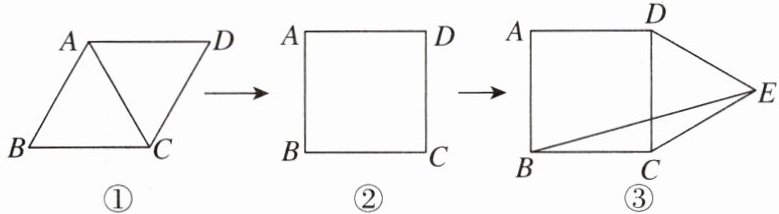
5. [2024昭通一模]如图,有六根长度相同的木条,小明先用四根木条制作了能够活动的菱形学具,他先将该活动学具调成如图①所示的菱形,测得$∠B= 60^{\circ }$,连接AC,$AC= 10cm$,接着将该活动学具调成如图②所示的正方形,最后用剩下的两根木条搭成了如图③所示的图形,连接BE,则图③中$\triangle BCE$的面积为( )
A. $50\sqrt {3}cm^{2}$
B. $50cm^{2}$
C. $25\sqrt {3}cm^{2}$
D. $25cm^{2}$


A. $50\sqrt {3}cm^{2}$
B. $50cm^{2}$
C. $25\sqrt {3}cm^{2}$
D. $25cm^{2}$
答案:
D [点拨]
∵菱形ABCD中,AB = BC,∠B = 60°,
∴△ABC是等边三角形。
∴AC = BC。
∵AC = 10cm。
∴BC = 10cm,
∴CE = BC = 10cm。
如图,过点E作EH⊥BC,交BC的延长线于点H,
易知△DCE是等边三角形,
∴∠DCE = 60°,
∴易得∠ECH = 30°,
∴EH = $\frac{1}{2}$CE = 5cm,
∴△BCE的面积 = $\frac{1}{2}$BC·EH = $\frac{1}{2}$×10×5 = 25(cm²),故选D。

D [点拨]
∵菱形ABCD中,AB = BC,∠B = 60°,
∴△ABC是等边三角形。
∴AC = BC。
∵AC = 10cm。
∴BC = 10cm,
∴CE = BC = 10cm。
如图,过点E作EH⊥BC,交BC的延长线于点H,
易知△DCE是等边三角形,
∴∠DCE = 60°,
∴易得∠ECH = 30°,
∴EH = $\frac{1}{2}$CE = 5cm,
∴△BCE的面积 = $\frac{1}{2}$BC·EH = $\frac{1}{2}$×10×5 = 25(cm²),故选D。

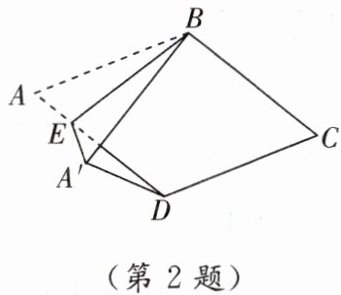
6. 新趋势·学科内综合 如图,在平面直角坐标系中,菱形OABC的边长为$2\sqrt {6}$,点B在x轴的正半轴上,且$∠AOC= 60^{\circ }$,将菱形OABC绕原点O逆时针方向旋转$60^{\circ }$,得到四边形$OA'B'C'$(点$A'$与点C重合),则点$B'$的坐标是( )

A. $(3\sqrt {6},3\sqrt {2})$
B. $(3\sqrt {2},3\sqrt {6})$
C. $(3\sqrt {2},6\sqrt {2})$
D. $(6\sqrt {2},3\sqrt {6})$

A. $(3\sqrt {6},3\sqrt {2})$
B. $(3\sqrt {2},3\sqrt {6})$
C. $(3\sqrt {2},6\sqrt {2})$
D. $(6\sqrt {2},3\sqrt {6})$
答案:
B [点拨]如图,延长B'C交x轴于点D,连接OB'。
∵四边形ABCO是菱形,点B在x轴的正半轴上,∠AOC = 60°,
∴∠COB = ∠AOB = 30°,∠CBA = 60°。
由旋转可得∠BOB' = 60°,∠C'B'C = ∠CBA = 60°,AB = CB'。
∴∠OB'D = $\frac{1}{2}$∠C'B'C = 30°。
∴∠B'DO = 90°。
在Rt△CDO中,OC = B'C = 2$\sqrt{6}$,
∴CD = $\frac{1}{2}$OC = $\sqrt{6}$。
∴OD = $\sqrt{3}$CD = $\sqrt{3}$×$\sqrt{6}$ = 3$\sqrt{2}$,DB' = 3$\sqrt{6}$。
∴B'(3$\sqrt{2}$, $\sqrt{6}$)。

B [点拨]如图,延长B'C交x轴于点D,连接OB'。
∵四边形ABCO是菱形,点B在x轴的正半轴上,∠AOC = 60°,
∴∠COB = ∠AOB = 30°,∠CBA = 60°。
由旋转可得∠BOB' = 60°,∠C'B'C = ∠CBA = 60°,AB = CB'。
∴∠OB'D = $\frac{1}{2}$∠C'B'C = 30°。
∴∠B'DO = 90°。
在Rt△CDO中,OC = B'C = 2$\sqrt{6}$,
∴CD = $\frac{1}{2}$OC = $\sqrt{6}$。
∴OD = $\sqrt{3}$CD = $\sqrt{3}$×$\sqrt{6}$ = 3$\sqrt{2}$,DB' = 3$\sqrt{6}$。
∴B'(3$\sqrt{2}$, $\sqrt{6}$)。

7. [2023重庆]如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,$BE= BA$,连接CE并延长,与$∠ABE$的平分线交于点F,连接OF.若$AB= 2$,则OF的长度为(
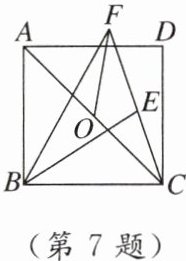
A. 2
B. $\sqrt {3}$
C. 1
D. $\sqrt {2}$
D
)
A. 2
B. $\sqrt {3}$
C. 1
D. $\sqrt {2}$
答案:
D [点拨]连接AF,根据正方形ABCD得到AB = BC = BE,∠ABC = 90°,根据勾股定理求得AC的长。根据角平分线的定义和等腰三角形的性质,求得∠BFE = 45°,再证明△ABF≌△EBF,求得∠AFC = 90°,最后根据直角三角形斜边上的中线等于斜边的一半,即可求出OF的长度。
8. 新视角 条件开放题 如图,在矩形ABCD中,对角线AC,BD相交于点O.试添加一个条件:

AB = AD(答案不唯一)
,使得矩形ABCD为正方形.
答案:
AB = AD(答案不唯一)
查看更多完整答案,请扫码查看


