第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. [2024上海奉贤区模拟]正方形具有而菱形不一定具有的性质是(
A. 对角线相等
B. 对角线互相垂直
C. 对角线平分一组对角
D. 对角线互相平分
A
)A. 对角线相等
B. 对角线互相垂直
C. 对角线平分一组对角
D. 对角线互相平分
答案:
A
2. [2023广州南沙区期末]一个正方形在平面直角坐标系中的三个顶点的坐标为$(-3,3),(-3,-1),(1,-1)$,则第四个顶点到x轴的距离是(
A. 1
B. 2
C. 3
D. 4
C
)A. 1
B. 2
C. 3
D. 4
答案:
C
3. 一个正方形和两个等边三角形的位置如图所示,若$∠3= 50^{\circ }$,则$∠1+∠2=$(

A. $90^{\circ }$
B. $100^{\circ }$
C. $130^{\circ }$
D. $180^{\circ }$
B
)
A. $90^{\circ }$
B. $100^{\circ }$
C. $130^{\circ }$
D. $180^{\circ }$
答案:
B
4. [2023河北]如图,在$Rt\triangle ABC$中,$AB= 4$,点M是斜边BC的中点,以AM为边作正方形AMEF.若$S_{正方形AMEF}= 16$,则$S_{\triangle ABC}= $(

A. $4\sqrt {3}$
B. $8\sqrt {3}$
C. 12
D. 16
B
)
A. $4\sqrt {3}$
B. $8\sqrt {3}$
C. 12
D. 16
答案:
B
5. 如图,点P是正方形ABCD内位于对角线AC下方的一点,$∠1= ∠2$,则$∠BPC$的度数为______

135
$^{\circ }$.
答案:
135
6. 母题教材P22习题T3如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作$BG⊥AE$,垂足为点G,延长BG交CD于点F.
求证:$BE= CF$.
[证明]∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=
∴∠BAE+∠AEB=
∵BG⊥AE,
∴∠BGE=
∴∠AEB+∠EBG=
∴∠BAE=∠EBG.
∴△ABE≌△BCF(
∴BE=CF.
求证:$BE= CF$.
[证明]∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=
90°
.∴∠BAE+∠AEB=
90°
.∵BG⊥AE,
∴∠BGE=
90°
.∴∠AEB+∠EBG=
90°
.∴∠BAE=∠EBG.
∴△ABE≌△BCF(
ASA
).∴BE=CF.
答案:
[证明]
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF.
∴∠BAE+∠AEB=90°.
∵BG⊥AE,
∴∠BGE=90°.
∴∠AEB+∠EBG=90°.
∴∠BAE=∠EBG.
∴△ABE≌△BCF(ASA).
∴BE=CF.
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF.
∴∠BAE+∠AEB=90°.
∵BG⊥AE,
∴∠BGE=90°.
∴∠AEB+∠EBG=90°.
∴∠BAE=∠EBG.
∴△ABE≌△BCF(ASA).
∴BE=CF.
7. [2023常德]如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且$EF// AD$,连接AF,DE.若$∠FAC= 15^{\circ }$,则$∠AED$的度数为(

A. $80^{\circ }$
B. $90^{\circ }$
C. $105^{\circ }$
D. $115^{\circ }$
C
)
A. $80^{\circ }$
B. $90^{\circ }$
C. $105^{\circ }$
D. $115^{\circ }$
答案:
C
8. 新视角·动点探究题[2024·汕头澄海区期末]如图,在平面直角坐标系中,正方形ABCD的两个顶点A,B是坐标轴上的动点,若正方形的边长为4,则线段OC长的最大值是(

A. $2+2\sqrt {3}$
B. $2+2\sqrt {5}$
C. $4\sqrt {2}$
D. 8
B
)
A. $2+2\sqrt {3}$
B. $2+2\sqrt {5}$
C. $4\sqrt {2}$
D. 8
答案:
B
9. 易错题如图,已知正方形ABCD的边长为2,P是对角线BD上一点,$PE⊥BC$于点E,$PF⊥CD$于点F,连接AP,EF.给出下列结论:
①$PD= \sqrt {2}EC$;
②四边形PECF的周长为4;
③$\triangle APD$一定是等腰三角形;
④$AP= EF$;
⑤EF的最小值为$\sqrt {2}$.
其中正确结论的序号为(
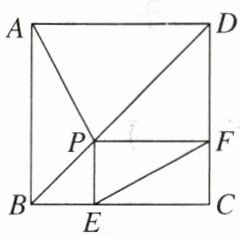
A. ①②③④
B. ①②④⑤
C. ②④⑤
D. ①②④
①$PD= \sqrt {2}EC$;
②四边形PECF的周长为4;
③$\triangle APD$一定是等腰三角形;
④$AP= EF$;
⑤EF的最小值为$\sqrt {2}$.
其中正确结论的序号为(
B
)
A. ①②③④
B. ①②④⑤
C. ②④⑤
D. ①②④
答案:
B [点拨]①
∵四边形ABCD是正方形,
∴∠BDC=45°,∠BCD=90°.
∵PE⊥BC,PF⊥CD,
∴∠PEC=∠PFC=PFD=90°.
∴四边形PECF是矩形,∠PDF=∠DPF=45°.
∴PF=EC,PF=DF.
∴在Rt△DPF中,PD²=DF²+PF²=EC²+EC²=2EC²,
∴PD=√2EC.
故①正确;
②
∵四边形PECF为矩形,PF=DF,
∴四边形PECF的周长=2CF+2PF=2CF+2DF=2DC =4.
故②正确;
③
∵点P是正方形ABCD的对角线BD上任意一点,
∴∠ADP=45°.由题意可知点P与点B不重合.
∴当∠PAD=45°或67.5°时,△APD是等腰三角形.
除此之外,△APD不是等腰三角形.
故③错误;
④连接PC,
∵四边形PECF为矩形,
∴PC=EF.
∵直线BD是正方形ABCD的对称轴,
∴AP=PC.
∴AP=EF.
故④正确;
⑤
∵EF=PC=AP,
∴当AP的长最小时,EF的长最小.
当AP⊥BD时,AP的长最小.
∵AB=AD=2,∠BAD=90°,
∴AP的长的最小值为1/2 BD=1/2 ×√(2²+2² )=√2,
即EF的长的最小值等于√2.
故⑤正确;故选B.
∵四边形ABCD是正方形,
∴∠BDC=45°,∠BCD=90°.
∵PE⊥BC,PF⊥CD,
∴∠PEC=∠PFC=PFD=90°.
∴四边形PECF是矩形,∠PDF=∠DPF=45°.
∴PF=EC,PF=DF.
∴在Rt△DPF中,PD²=DF²+PF²=EC²+EC²=2EC²,
∴PD=√2EC.
故①正确;
②
∵四边形PECF为矩形,PF=DF,
∴四边形PECF的周长=2CF+2PF=2CF+2DF=2DC =4.
故②正确;
③
∵点P是正方形ABCD的对角线BD上任意一点,
∴∠ADP=45°.由题意可知点P与点B不重合.
∴当∠PAD=45°或67.5°时,△APD是等腰三角形.
除此之外,△APD不是等腰三角形.
故③错误;
④连接PC,
∵四边形PECF为矩形,
∴PC=EF.
∵直线BD是正方形ABCD的对称轴,
∴AP=PC.
∴AP=EF.
故④正确;
⑤
∵EF=PC=AP,
∴当AP的长最小时,EF的长最小.
当AP⊥BD时,AP的长最小.
∵AB=AD=2,∠BAD=90°,
∴AP的长的最小值为1/2 BD=1/2 ×√(2²+2² )=√2,
即EF的长的最小值等于√2.
故⑤正确;故选B.
查看更多完整答案,请扫码查看


