《2025年综合应用创新题典中点九年级数学上册北师大版》

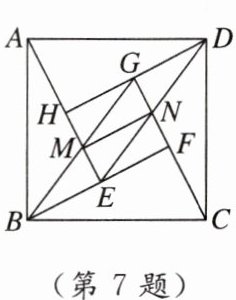
7. 如图所示为“赵爽弦图”,其中$\triangle ABE,\triangle CBF,\triangle CDG,\triangle ADH$是四个全等的直角三角形,且两条直角边长之比为$1:2$,连接BG,DE,分别交AE,CG于点M,N,连接MN,则四边形GBED和四边形GMEN的面积比为 (B)

A. $5:2$
B. $2:1$
C. $\sqrt {2}:1$
D. $\sqrt {3}:1$

答案： B

8. [2024常德鼎城区模拟]如图,在$\triangle ABC$中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线于点F,且$AF= BD$,连接BF.
(1)求证:$BD= CD;$
证明：$ \because AF // BC $，
$ \therefore \angle AFE = \angle ECD $。
$ \because E $ 是 $ AD $ 的中点，$ \therefore DE = AE $。
在 $ \triangle AEF $ 与 $ \triangle DEC $ 中，$ \left\{ \begin{array} { l } { \angle AFE = \angle ECD, } \\ { \angle AEF = \angle DEC, } \\ { AE = ED, } \end{array} \right. $
$ \therefore \triangle AEF \cong \triangle DEC ( \text { AAS } ) $。$ \therefore AF = DC $。
$ \because AF = BD $，
$ \therefore BD = CD $。
(2)如果$AB= AC$,试判断四边形AFBD的形状,并证明你的结论;
四边形AFBD的形状为矩形
证明：$ \because AF = BD $，$ AF // BD $，
$ \therefore $ 四边形 $ AFBD $ 为平行四边形。
$ \because AB = AC $，$ BD = DC $，
$ \therefore AD \perp BC $。$ \therefore \angle BDA = 90 ^ { \circ } $。
$ \therefore $ 四边形 $ AFBD $ 为矩形。
(3)当$\triangle ABC$满足什么条件时,四边形AFBD为正方形? (写出条件即可,不要求证明)
当$\triangle ABC$满足$AB= AC$，且$\angle BAC= 90^{\circ}$时，四边形AFBD为正方形。

答案：
(1) 【证明】$ \because AF // BC $，
$ \therefore \angle AFE = \angle ECD $。
$ \because E $ 是 $ AD $ 的中点，$ \therefore DE = AE $。
在 $ \triangle AEF $ 与 $ \triangle DEC $ 中，$ \left\{ \begin{array} { l } { \angle AFE = \angle ECD, } \\ { \angle AEF = \angle DEC, } \\ { AE = ED, } \end{array} \right. $
$ \therefore \triangle AEF \cong \triangle DEC ( \text { AAS } ) $。$ \therefore AF = DC $。
$ \because AF = BD $，
$ \therefore BD = CD $。
(2) 【解】四边形 $ AFBD $ 为矩形。
证明：$ \because AF = BD $，$ AF // BD $，
$ \therefore $ 四边形 $ AFBD $ 为平行四边形。
$ \because AB = AC $，$ BD = DC $，
$ \therefore AD \perp BC $。$ \therefore \angle BDA = 90 ^ { \circ } $。
$ \therefore $ 四边形 $ AFBD $ 为矩形。
(3) 【解】当 $ \triangle ABC $ 满足 $ AB = AC $，且 $ \angle BAC = 90 ^ { \circ } $ 时，四边形 $ AFBD $ 为正方形。（答案不唯一）

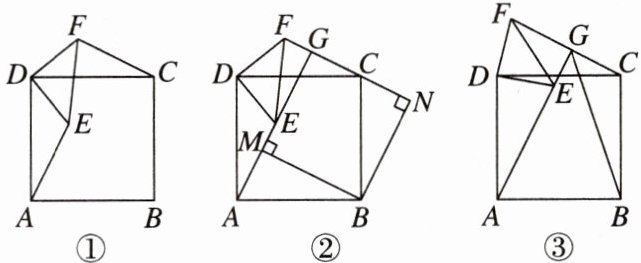
9. 新考法 特殊位置法 已知四边形ABCD是正方形,$\triangle DEF$绕点D旋转$(DE\lt AB),∠EDF= 90^{\circ },DE= DF$,连接AE,CF.
(1)如图①,求证:$\triangle ADE\cong \triangle CDF;$
(2)直线AE与CF相交于点G.
①如图②,$BM⊥AG$于点M,$BN⊥CF$于点N,求证:四边形BMGN是正方形;
②如图③,连接BG,若$AB= 4,DE= 2$,直接写出在$\triangle DEF$旋转的过程中,线段BG长度的最小值.$2\sqrt{6}$

答案：
(1) 【证明】$ \because $ 四边形 $ ABCD $ 是正方形，
$ \therefore AD = DC $，$ \angle ADC = 90 ^ { \circ } $。
$ \because \angle EDF = 90 ^ { \circ } $，$ \therefore \angle ADC = \angle EDF $。
$ \therefore \angle ADE = \angle CDF $。
在 $ \triangle ADE $ 和 $ \triangle CDF $ 中，$ \left\{ \begin{array} { l } { D A = D C, } \\ { \angle A D E = \angle C D F, } \\ { D E = D F, } \end{array} \right. $
$ \therefore \triangle ADE \cong \triangle CDF ( \text { SAS } ) $。
(2) ① 【证明】设 $ AG $ 与 $ CD $ 相交于点 $ P $。
$ \because \angle ADP = 90 ^ { \circ } $，
$ \therefore \angle DAP + \angle DPA = 90 ^ { \circ } $。
$ \because \triangle ADE \cong \triangle CDF $，
$ \therefore \angle DAE = \angle DCF $。
又 $ \because \angle DPA = \angle GPC $，
$ \therefore \angle GPC + \angle GCP = \angle DAE + \angle DPA = 90 ^ { \circ } $。
$ \therefore \angle PGN = 90 ^ { \circ } $。
又 $ \because BM \perp AG $，$ BN \perp GN $，$ \therefore \angle BMG = \angle BNG = 90 ^ { \circ } $。
$ \therefore $ 四边形 $ BMGN $ 是矩形。
$ \therefore \angle MBN = 90 ^ { \circ } $。
$ \because $ 四边形 $ ABCD $ 是正方形，
$ \therefore AB = BC $，$ \angle ABC = 90 ^ { \circ } = \angle MBN $。
$ \therefore \angle ABM = \angle CBN $。
又 $ \because \angle AMB = \angle BNC = 90 ^ { \circ } $，$ \therefore \triangle AMB \cong \triangle CNB $。
$ \therefore MB = NB $。
$ \therefore $ 矩形 $ BMGN $ 是正方形。
② 【解】线段 $ BG $ 长度的最小值为 $ 2 \sqrt { 6 } $。