《2025年综合应用创新题典中点九年级数学上册北师大版》

11. [2023泰安]如图,在△ABC中,AC= BC= 16,点D在AB上,点E在BC上,点B关于直线DE的轴对称点为点B',连接DB',EB',分别与AC相交于F点、G点,若AF= 8,DF= 7,B'F= 4,则CG的长度为______4.5．

答案： 4.5 [点拨]
∵AC=BC=16，
∴∠A=∠B.
　　由折叠的性质可得∠B=∠B'，
∴∠A=∠B'.
　又
∵∠AFD=∠B'FG，
∴△AFD∽△B'FG.
　
∴$\frac{AF}{B'F}=\frac{DF}{GF}$，即$\frac{8}{4}=\frac{7}{GF}$，解得GF=3.5.
　
∴CG=AC−AF−GF=4.5.

12. 如图,在Rt△ABC中,∠C= 90°,AC= 3,BC= 1,将△ABC绕点A逆时针方向旋转90°,得到△AB'C'．连接BB',交AC于点D,则$\frac{AD}{DC}$的值为______．

答案：
5 [点拨]如图，过点D作DF⊥AB于点F，则∠AFD=90°，
　　　　　　　　　
　
∴∠C=∠AFD=90°.
　
∵∠ACB=90°，AC=3，BC=1，
　
∴AB=$\sqrt{3^{2}+1^{2}}=\sqrt{10}$
　
∵将△ABC绕点A逆时针方向旋转90°得到△AB'C'，
∴∠BAB'=90°.
　
∴△ABB'是等腰直角三角形.
∴∠ABB'=45°.
　　又
∵DF⊥AB，
∴∠FDB=45°，
　
∴△DFB是等腰直角三角形.
∴DF=BF.
　
∵S△ADB=$\frac{1}{2}$AD·BC=$\frac{1}{2}$AB·DF，
　
∴AD=$\sqrt{10}$DF.
　
∵∠C=∠AFD=90°，∠CAB=∠FAD，
　
∴△AFD∽△ACB.
　
∴$\frac{DF}{BC}=\frac{AF}{AC}$，即$\frac{DF}{1}=\frac{AF}{3}$，
∴AF=3DF.
　　又
∵AF=$\sqrt{10}$−DF，
∴DF=$\frac{\sqrt{10}}{4}$.
　
∴AD=$\sqrt{10}\times\frac{\sqrt{10}}{4}=\frac{5}{2}$，
∴DC=3−$\frac{5}{2}=\frac{1}{2}$.
　
∴$\frac{AD}{DC}=\frac{\frac{5}{2}}{\frac{1}{2}}=5$.

13. (14分)[2023佛山顺德区期中]如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点都在格点上,其坐标分别为A(-4,-4),B(6,-6),C(0,-2)．

(1)请以点O为位似中心,画出符合条件的△ABC的所有位似图形,使之与△ABC的相似比为1:2．
(2)△ABC内一点P(m,n),经过如此位似变化后,对应点的坐标是______．

答案：
[解]
(1)如图所示，△A₁B₁C₁，△A₂B₂C₂为所求.
　　　　　　　
(2)$(\frac{1}{2}m,\frac{1}{2}n)$或$(-\frac{1}{2}m,-\frac{1}{2}n)$

14. (16分)[2024西安辅轮中学月考]乐乐去西安旅游,当他看见宏伟的古城墙后,他想要测量城墙的高度．如图,他拿着一根笔直的小棍BC,站在距城墙约30m的点N处(即EN= 30m),把手臂向前伸直且让小棍BC竖直,BC//DE,乐乐看到点B和城墙顶端D在一条直线上,点C和底端E在一条直线上．已知乐乐的臂长CM约为60cm,小棍BC的长为24cm,AN⊥EN,CM⊥AN,DE⊥EN,求城墙的高度DE．

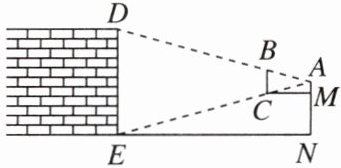
答案：
[解]如图，过点A作AH⊥DE于点H，交BC于点G.
　　　　　　　　
　则AG=CM=60厘米=0.6米，AH=NE=30米.
　由题意得BC=24厘米=0.24米，BC//DE，
∴∠ABC=∠ADE，∠ACB=∠AED.
∴△ABC∽△ADE.
∴$\frac{BC}{DE}=\frac{AG}{AH}$，即$\frac{0.24}{DE}=\frac{0.6}{30}$，解得DE=12米.
　因此，城墙的高度DE为12米.

15. (18分)如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABC= 2∠BAM．
(1)求证：AG= BG；
(2)若M为BC的中点,S△BGM= 1,求△ADG的面积．

(1)[证明]∵四边形ABCD为菱形，∴BD平分∠ABC. ∴∠ABC=2∠ABG.
　又∵∠ABC=2∠BAM，∴∠BAG=∠ABG.
　　∴AG=BG.
(2)[解]∵四边形ABCD为菱形，∴AD//BC，AD=BC. ∴∠GAD=∠GMB.
　又∵∠AGD=∠BGM，∴△BGM∽△DGA.
　∵M为BC的中点，∴BM=$\frac{1}{2}$BC=$\frac{1}{2}$AD.
　∴$\frac{BM}{AD}=\frac{1}{2}$.
　∴△BGM与△DGA的相似比为1:2.
　∴S△BGM:S△ADG=1:4.
　∵S△BGM=1，∴S△ADG=4.

答案：
(1)[证明]
∵四边形ABCD为菱形，
∴BD平分∠ABC.
∴∠ABC=2∠ABG.
　又
∵∠ABC=2∠BAM，
∴∠BAG=∠ABG.
　
∴AG=BG.
(2)[解]
∵四边形ABCD为菱形，
∴AD//BC，AD=BC.
∴∠GAD=∠GMB.
　又
∵∠AGD=∠BGM，
∴△BGM∽△DGA.
∵M为BC的中点，
∴BM=$\frac{1}{2}$BC=$\frac{1}{2}$AD.
∴$\frac{BM}{AD}=\frac{1}{2}$.
∴△BGM与△DGA的相似比为1:2.
∴S△BGM:S△ADG=1:4.
∵S△BGM=1，
∴S△ADG=4.