《2025年综合应用创新题典中点九年级数学上册北师大版》

1. 2024·郑州金水区模拟 母题·教材P8做一做 如图,剪两张等宽且对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,连接AC,BD,其中一张纸条在转动过程中,下列结论一定成立的是(B)

A. 四边形ABCD的周长不变
B. $ AB = BC $
C. 四边形ABCD的面积不变
D. $ AC = BD $

答案： B

2. [2023永州期末]如图,四边形ABCD为菱形,A,B两点的坐标分别是$ (\sqrt{3},0) $,$ (0,1) $,点C,D在坐标轴上,则菱形ABCD的面积等于(B)

A. $ 4\sqrt{3} $
B. $ 2\sqrt{3} $
C. $ \sqrt{3} $
D. $ \frac{\sqrt{3}}{2} $

答案： B

3. 如图,平行四边形ABCD中,$ ∠A = 110^{\circ} $,$ AD = DC $. E,F分别是边AB和BC的中点,$ EP⊥CD $于点P,则$ ∠PEF = $(35°)

A. $ 35^{\circ} $
B. $ 45^{\circ} $
C. $ 50^{\circ} $
D. $ 55^{\circ} $

答案： A　[点拨]
∵平行四边形ABCD中，AD=DC,
∴四边形ABCD为菱形，AD//BC,AB//CD.
∴AB=BC,∠ABC=180°−∠A=70°.
∵E,F分别为AB,BC的中点，
∴BE=$\frac{1}{2}$AB,BF=$\frac{1}{2}$BC.
∴BE=BF.
∴∠BEF=∠BFE=55°,
∵PE⊥CD,AB//CD,
∴PE⊥AB.
∴∠PEB=90°,
∴∠PEF=90°−55°=35°.

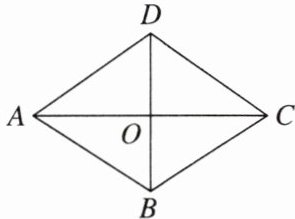
4. 母题教材P6例2 如图,平行四边形ABCD的两条对角线相交于点O,$ OA = 3 $,$ OB = 2 $,$ AB = \sqrt{13} $.
(1)求证：平行四边形ABCD是菱形；
证明：在△AOB中，OA=3，OB=2，AB=√13，∴OA²+OB²=9+4=13=AB².∴△AOB是直角三角形，且∠AOB=90°.∴AC⊥BD.又∵四边形ABCD是平行四边形，∴平行四边形ABCD是菱形.
(2)求菱形ABCD的面积.
解：∵四边形ABCD是菱形，∴AC=2OA=6，BD=2OB=4.∴S_{菱形ABCD}=1/2AC·BD=12.

答案： $(1)[$证明$]$在$△AOB$中$,OA=3,OB=2,AB= \sqrt{13},$　　
$　$
∴$OA²+OB²=9+4=13=AB².$　　
$　$
∴$△AOB$是直角三角形，且$∠AOB=90°.$　　
$　$
∴$AC⊥BD.$　　
$　$又
∵四边形$ABCD$是平行四边形，　　
$　$
∴平行四边形$ABCD$是菱形$.$　　
$(2)[$解$]$
∵四边形$ABCD$是菱形，　　
$ $
∴$AC=2OA=6,BD=2OB=4.$　　
$ $
∴$S_{菱形ABCD}=\frac{1}{2}AC·BD=12.$　　

5. 如图①,在菱形ABCD中,对角线AC,BD相交于O,要在对角线BD上找两点M,N,使得四边形AMCN是菱形,现有图②中的甲、乙两种方案,则正确的方案是(C)

A. 只有甲
B. 只有乙
C. 甲和乙
D. 甲、乙都不是

答案： C

6. 新视角·动点探究题 2023·德阳 如图,$ □ ABCD $的面积为12,$ AC = BD = 6 $,AC与BD交于点O,分别过点C,D作BD,AC的平行线相交于点F,点G是CD的中点,点P是四边形OCFD边上的动点,则PG的最小值是( )

A. 1
B. $ \frac{\sqrt{3}}{2} $
C. $ \frac{3}{2} $
D. 3

答案：
A　[点拨]
∵DF//AC,CF//BD,
∴四边形OCFD是平行四边形,
∵四边形ABCD为平行四边形，
∴OD=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AC.
　又
∵AC=BD,
∴OD=OC.
∴四边形OCFD为菱形.
∵点G是CD的中点，点P是四边形OCFD边上的动点，
∴当GP垂直于菱形OCFD的一边时,PG有最小值.
　如图,过D点作DM⊥AC于点M,过G点作GP⊥AC于点P,则GP//MD.
∵平行四边形ABCD的面积为12,AC=6，
∴2×$\frac{1}{2}$AC×DM=12,
即2×$\frac{1}{2}$×6×DM=12,
　解得DM=2.
　由G为CD的中点，易知GP为△DMC的中位线.
∴GP=$\frac{1}{2}$DM=1,故PG的最小值为1.

7. 易错题 如图,在菱形ABCD中,$ ∠BAD = 60^{\circ} $,AC与BD交于点O,E为CD延长线上的一点,且$ DE = CD $,连接BE分别交AC,AD于点F,G,连接OG,则下列结论：
①$ OG = \frac{1}{2}AB $；
②与$ △DEG $全等的三角形共有5个；
③四边形ODEG与四边形OBAG的面积相等；
④由点A,B,D,E构成的四边形是菱形.
其中一定成立的是(A)

A. ①③④
B. ①②③
C. ①②④
D. ②③④

答案： A