《2025年畅行课堂七年级数学下册北师大版》

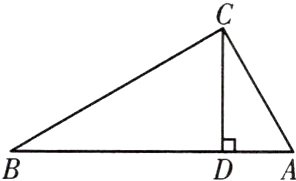
9.(教材P93习题T4变式)如图,已知∠ACB =90°,CD⊥AB,垂足是D,则图中与∠B互余的角有　　　　　　　　　　　　　　　(　　)
　　　　　　
　
A.1个　　
　B.2个　　
　C.3个　　
　D.4个

答案： B

10.如图,已知∠AOD=30°,点C是射线OD 上的一个动点，在点C的运动过程中，△AOC恰好是直角三角形,则此时∠A所有可能的度数为________。
　　　　　　

[点拨]由于直角顶点不确定，故要分类讨论，即①点
A是直角顶点;②点C是直角顶点。

答案： 60°或90°

11.(教材P86“思考.交流”变式)下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是　　　　　　　　(　　)
　

答案： A

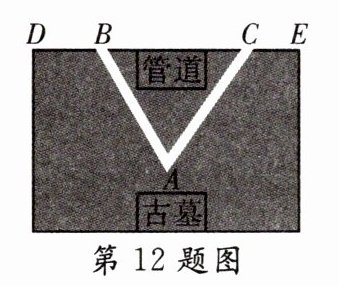
12.[真实问题情境]如图，考古学家发现在地下A处有一座古墓，古墓上方是燃气管道，为了不影响管道，准备在B和C处开工挖出“V”字形通道。若∠DBA=120°,∠ECA=125°,则∠A的度数是　　　(　　)
　
A.65°　
　B.80°　　
　C.85°　　
　D.90°

答案： A

13.如图,直线a//b,将Rtt△ABC按如图所示的方式放置。若∠1=28°,∠2=80°,则∠B的度数为　　　　　　　　　　　　(　　)
　
A.62°　
　B.52°　　
　C.38°　　
　D.28°

答案： C

14.将一副三角板按图中的方式叠放,则角α等于　　　　　　　　　　　　　　　　(　　)
　
A.105°　　B.60°　　　C.45°　　　D.30°
　　　

答案： A

[变式]将一副直角三角板如图摆放，点C 在EF上,AC经过点D,∠A=∠EDF=
　90°,∠BCE=40°,则∠CDF=________。

答案： 25°

15.(2024.凉山州)如图,△ABC中，∠BCD =30°,∠ACB=80°,CD是边AB上的高，
AE是∠CAB的平分线,则∠AEB的度数是________.
　　　　　　

答案： 100°

16.如图,在△ABC中,∠A=60°,∠ACB=
　　40°,点D为BC延长线上一点，∠ABM=
　　∠CBM,点E为射线BM上一点，连接CE。
　　(1)若CE//AB,求∠BEC的度数;
　　(2)若∠ACE=∠BCE,则∠BEC=________。
　　　

答案： 解:
(1)因为∠A = 60°，∠ACB = 40°，
所以∠ABC = 80°，
所以∠ABM = ∠CBM = $\frac{1}{2}$∠ABC = 40°。
因为CE//AB，
所以∠BEC = ∠ABE = 40°。
(2)120°

17.[分类讨论思想]已知∠AOB=40°,点C,D 分别是射线OA,OB上的一点，且DC⊥OA,点E为线段OD上的一个动点(不与点O,D 重合),当△CED中有两个相等的角时，∠OCE的度数为____________。

答案： 10°或40°或25°