第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图,在△ABC中,∠C = 90°,点D在AC上,DE//AB。若∠CDE = 160°,则∠B的度数为 ( )
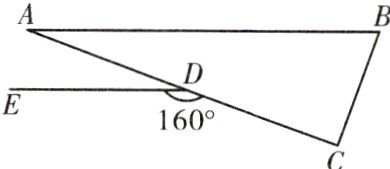
A. 40°
B. 50°
C. 60°
D. 70°

A. 40°
B. 50°
C. 60°
D. 70°
答案:
D
2. 如图,一只手握住了一个三角形的一部分,则这个三角形是 ( )
A. 钝角三角形
B. 直角三角形
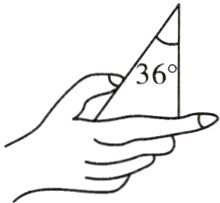
C. 锐角三角形
D. 以上都有可能
A. 钝角三角形
B. 直角三角形

C. 锐角三角形
D. 以上都有可能
答案:
D
3. 如图,∠ABC = 50°,点D,E分别在射线BA,BC上,将△BED沿DE折叠,若点B恰好落在射线BA上的点B'处,则∠BEB'的度数为 ( )
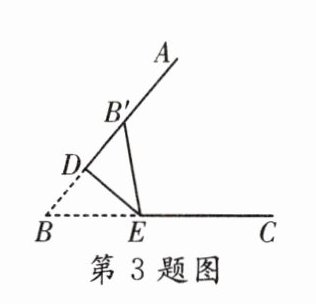
A. 50°
B. 80°
C. 100°
D. 130°

A. 50°
B. 80°
C. 100°
D. 130°
答案:
B
4. 如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AB于点E。若∠B = 50°,∠ACE = 20°,则∠ADC的度数是________。
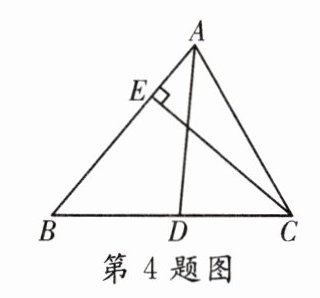

答案:
85°
5. (株洲中考)《周礼.考工记》中记载有:“……半矩谓之宣(xuan),一宣有半谓之橘(zhú)”。意思是:“……直角的一半的角叫做宣,一宣半的角叫做橘……”。即1宣 = $\frac{1}{2}$矩,1橘 = 1$\frac{1}{2}$宣(1矩 = 90°)。
问题:图1为中国古代一种强弩图,图2为这种强弩图的部分组件的示意图。若∠A = 1矩,∠B = 1橘,则∠C =______度。

问题:图1为中国古代一种强弩图,图2为这种强弩图的部分组件的示意图。若∠A = 1矩,∠B = 1橘,则∠C =______度。

答案:
22.5
6. 劳动课上,小莉要用三根木棒首尾相接钉一个三角形框架。已知两根木棒的长分别为4cm,5cm,则第三根木棒的长可以为( )
A. 1cm
B. 4cm
C. 9cm
D. 10cm
A. 1cm
B. 4cm
C. 9cm
D. 10cm
答案:
B
7. 若一个三角形两条边的长分别是4和6,第三条边的长是整数,则该三角形周长的最大值是______。
答案:
19
8. 如图,AD,AE,AF分别是△ABC的高、角平分线和中线。
(1)若S△ABC = 20,CF = 4,求AD的长;
(2)若∠C = 70°,∠B = 26°,求∠DAE的度数。

(1)若S△ABC = 20,CF = 4,求AD的长;
(2)若∠C = 70°,∠B = 26°,求∠DAE的度数。

答案:
解:
(1)因为AF是△ABC的中线,所以BF=CF=4,所以BC=8。因为S△ABC = 20,
所以$\frac{1}{2}$BC·AD = 20,
即$\frac{1}{2}$×8×AD = 20,
所以AD = 5。
(2)因为∠C = 70°,∠B = 26°,
所以∠CAB = 180° - ∠B - ∠C = 84°。因为AE是△ABC的角平分线,所以∠CAE = $\frac{1}{2}$∠CAB = 42°。
因为∠ADC = 90°,∠C = 70°,
所以∠DAC = 20°,
所以∠DAE = ∠CAE - ∠DAC = 42° - 20° = 22°。
(1)因为AF是△ABC的中线,所以BF=CF=4,所以BC=8。因为S△ABC = 20,
所以$\frac{1}{2}$BC·AD = 20,
即$\frac{1}{2}$×8×AD = 20,
所以AD = 5。
(2)因为∠C = 70°,∠B = 26°,
所以∠CAB = 180° - ∠B - ∠C = 84°。因为AE是△ABC的角平分线,所以∠CAE = $\frac{1}{2}$∠CAB = 42°。
因为∠ADC = 90°,∠C = 70°,
所以∠DAC = 20°,
所以∠DAE = ∠CAE - ∠DAC = 42° - 20° = 22°。
查看更多完整答案,请扫码查看


