《2025年畅行课堂七年级数学下册北师大版》

1. (2024·湖北省卷)计算2x·3x²的结果是(　　)
A. 5x²　　
　B. 6x²　　
　C. 5x³　　
　D. 6x³

答案： D

2. 化简(－a)²·(－b)的结果是(　　)
A. −3ab　
　B. 3ab　　
　C. −a²b　
　D. a²b

答案： D

3. (陕西中考)计算：2x·(−3x²y²)=(　　)
A. −6x³y²　　　　　
　B. 6x³y²
C. −6x²y³　　　　　
　D. 18x²y³

答案： A

4. 若等式2a²·a + 　　 = 3a³成立，则　　中的单项式可以是(　　)
A. a　　　
　B. a²　　　
　C. a³　　　
　D. a

答案： C

5. 下列计算正确的是(　　)
A. 3x²·2x²y = 6x⁴y
B. 2.5a²·4a² = 10a⁴
C. (2x)²·(−5x²y) = −20x⁴y
D. −2xy·(−3x²y) = 6x³y²

答案： B

6. 如果xⁿy⁴与2xᵐy相乘的结果是2x⁵y⁵，那么mn = ______。

答案： 12

7. (1)[答题模板]−2a³b²·(3ab²)=(________×______).a³⁺(　).b²⁺(　)=________。
(2)[针对练习]①ab²·(−2a²b)；
②(−8ab²)·(−$\frac{1}{2}$a)³。

答案：
(1)−2　3　1　3　−6a²b²
(2)①解:原式=−2a²b²。
　②解:原式=(−8ab²)·(−$\frac{1}{8}$a³)
　　　　　=[(−8)×(−$\frac{1}{8}$)]·(a·a³)·b²
　　　　　=a⁴b²。

8. 如图，该图形的面积是(　　)

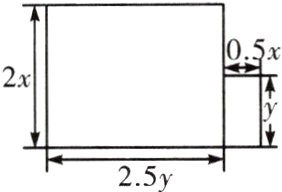
A. $\frac{11}{2}$xy　
　B. $\frac{13}{2}$xy　
　C. 6xy　　
　D. 3xy

答案： A

9. 一个三角形的底为4a，底边上的高为$\frac{1}{2}$a²，则它的面积为______。

答案： a²

10. 计算：(−3xy²)²·(−x²yz) = ____________。

答案： 27xy

11. 下列运算正确的是(　　)
A. (−2ab)·(−3ab)² = −18a³b³
B. 5x²·(3x²)² = 45x⁶
C. (−0.1b)·(−10b²)² = −10b⁵
D. (3×10ᵐ)×($\frac{1}{3}$×10ⁿ) = 10ᵐ⁺ⁿ

答案： D

12. 若ab² = −2，则(−3ab)·2ab² = ______。

答案： −24

13. (教材P16习题T1变式)计算：
(1)(−4x²y)·(−x²y²)·$\frac{1}{2}$y²；
(2)2x·(−3xy)²·(−x²y)²；
(3)(−3abc)·(−a²c²)²·(−5a²b)。

答案：
(1)解:原式=[(−4)×(−$\frac{1}{2}$)]×(x²·x³)·(y·y²·y³)
　　　　　　=2x⁵y⁶。
(2)解:原式=2x·9x²y²·(−x²y²)
　　　　　　=−18x⁵y⁴。
(3)解:原式=(−3abc)·a⁴c⁶·(−5a²b)
　　　　　　=[(−3)×(−5)]·(a·a⁴·a²)·(b·b)·(c·c⁶)
　　　　　　=15a⁷b²c⁷。