第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. [跨学科融合][几何直观、推理能力、应用意识]当光线从空气中射入水中时,光线的传播方向发生了变化,这种现象叫作光的折射。
如图,直线AB与CD相交于点F,一束光线沿CD射入水面,在点F处发生折射,沿FE射入水中。如果∠1 = 42°,∠2 = 29°,那么光线与AB的夹角改变了 ( )
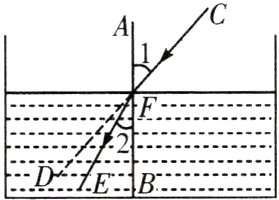
A. 10°
B. 12°
C. 13°
D. 15°
如图,直线AB与CD相交于点F,一束光线沿CD射入水面,在点F处发生折射,沿FE射入水中。如果∠1 = 42°,∠2 = 29°,那么光线与AB的夹角改变了 ( )

A. 10°
B. 12°
C. 13°
D. 15°
答案:
C
2. [几何直观、推理能力、创新意识]如图,点P是∠AOB的边OB上一点。
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)分别比较PH与PC,PC与CO,PH与CO的大小,并说明理由。

(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)分别比较PH与PC,PC与CO,PH与CO的大小,并说明理由。

答案:
解:
(1)如图,PH即为所求。

(2)如图,PC即为所求。
(3)PH<PC,PC<CO,PH<CO。理由:垂线段最短。
解:
(1)如图,PH即为所求。

(2)如图,PC即为所求。
(3)PH<PC,PC<CO,PH<CO。理由:垂线段最短。
3. [几何直观、空间观念、推理能力、模型观念]如图,将长方形纸片的一角折叠,使顶点A落在点A'处,折痕为BC。
(1)∠A'BC与∠ABC有怎样的数量关系?
(2)如果BE是∠A'BD的平分线,那么BE与BC有怎样的位置关系?为什么?

(1)∠A'BC与∠ABC有怎样的数量关系?
(2)如果BE是∠A'BD的平分线,那么BE与BC有怎样的位置关系?为什么?

答案:
解:
(1)由折叠的性质,得∠A'BC =∠ABC。
(2)BE⊥BC。理由如下:
由
(1),知∠A'BC=∠ABC,
因为BE平分∠A'BD,
所以∠A'BE=∠DBE。
又因为∠A'BC + ∠ABC + ∠A'BE + ∠DBE = 180°,所以∠A'BC + ∠A'BE = 90°,所以∠EBC = 90°,即BE⊥BC。
(1)由折叠的性质,得∠A'BC =∠ABC。
(2)BE⊥BC。理由如下:
由
(1),知∠A'BC=∠ABC,
因为BE平分∠A'BD,
所以∠A'BE=∠DBE。
又因为∠A'BC + ∠ABC + ∠A'BE + ∠DBE = 180°,所以∠A'BC + ∠A'BE = 90°,所以∠EBC = 90°,即BE⊥BC。
4. [几何直观、推理能力、模型观念]如图,直线AB,CD,EF被直线BF所截,∠B + ∠1 = 180°,∠2 = ∠3,试说明:∠B + ∠F = 180°。


答案:
解:因为∠B + ∠1 = 180°,
所以AB//CD。
因为∠2 = ∠3,
所以CD//EF,
所以AB//EF,
所以∠B + ∠F = 180°。
所以AB//CD。
因为∠2 = ∠3,
所以CD//EF,
所以AB//EF,
所以∠B + ∠F = 180°。
5. [几何直观、空间观念、推理能力、创新意识]如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在点D',C'的位置,ED'的延长线与BC相交于点G。设∠EFG = 68°,求∠1,∠2的度数。


答案:
解:由题意,得∠DEF = ∠D'EF,
AD//BC,
所以∠DEF = ∠EFG = 68°,
所以∠D'EF = 68°。
因为∠1 + ∠DEF + ∠D'EF = 180°,所以∠1 = 44°。
因为AD//BC,所以∠1 + ∠2 = 180°,所以∠2 = 180° - ∠1 = 136°。
AD//BC,
所以∠DEF = ∠EFG = 68°,
所以∠D'EF = 68°。
因为∠1 + ∠DEF + ∠D'EF = 180°,所以∠1 = 44°。
因为AD//BC,所以∠1 + ∠2 = 180°,所以∠2 = 180° - ∠1 = 136°。
6. [几何直观、推理能力、创新意识]试说明:两条平行线被第三条直线所截,同旁内角的平分线互相垂直。
答案:
解:题目可用数学语言表达为:如图,已知a//b,AC平分∠DAB,BC平分∠ABE,试说明:AC⊥BC。

说明过程如下:
如图,过点C作直线a的平行线CF。
因为a//b,所以a//CF//b,∠DAB + ∠ABE = 180°。
所以∠1 = ∠ACF,∠2 = ∠BCF。因为AC,BC分别是∠DAB,∠ABE的平分线,所以∠1 = $\frac{1}{2}$∠DAB,∠2 = $\frac{1}{2}$∠ABE,
所以∠ACF + ∠BCF = ∠1 + ∠2 = $\frac{1}{2}$×180° = 90°,即∠ACB = 90°,所以AC⊥BC,
所以两条平行线被第三条直线所截,同旁内角的平分线互相垂直。
解:题目可用数学语言表达为:如图,已知a//b,AC平分∠DAB,BC平分∠ABE,试说明:AC⊥BC。

说明过程如下:
如图,过点C作直线a的平行线CF。
因为a//b,所以a//CF//b,∠DAB + ∠ABE = 180°。
所以∠1 = ∠ACF,∠2 = ∠BCF。因为AC,BC分别是∠DAB,∠ABE的平分线,所以∠1 = $\frac{1}{2}$∠DAB,∠2 = $\frac{1}{2}$∠ABE,
所以∠ACF + ∠BCF = ∠1 + ∠2 = $\frac{1}{2}$×180° = 90°,即∠ACB = 90°,所以AC⊥BC,
所以两条平行线被第三条直线所截,同旁内角的平分线互相垂直。
查看更多完整答案,请扫码查看


