《2025年畅行课堂七年级数学下册北师大版》

二、与平行线的性质有关的计算
 

答案： 【教材母题】 解：因为a//b， 根据“两直线平行，内错角相等”，
所以∠2 = ∠1 = 107°
因为c//d， 根据“两直线平行，同旁内角互补”
所以∠1 + ∠3 = 180°
 所以∠3 = 180° - ∠1 = 180° - 107° = 73°

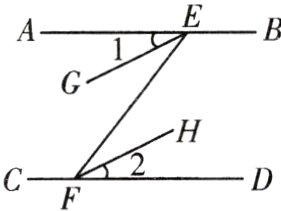
4. 已知:如图,EG//FH,∠1 = ∠2。
(1)试说明:∠BEF + ∠DFE = 180°;
(2)若EG平分∠AEF,且∠2 = 26°,求∠BEF的度数。

答案： 解:
(1)因为EG//HF，
所以∠FEG = ∠EFH。
因为∠1 = ∠2，
所以∠1 + ∠FEG = ∠2 + ∠EFH，
即∠AEF = ∠DFE，
所以AB//CD，
所以∠BEF + ∠DFE = 180°
(2)因为EG平分∠AEF，
所以∠AEF = 2∠1。
因为∠1 = ∠2 = 26°，
所以∠AEF = 2×26° = 52°，
所以∠BEF = 180° - ∠AEF
= 180° - 52°
= 128°。

5. 如图,已知AM//BN,∠A = 64°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D。
(1)∠ABN的度数是________;
(2)求∠CBD的度数;
(3)当点P运动时，∠APB与∠ADB之间的数量之比是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由;若变化，请写出变化规律。

答案： 解:
(1)116°
(2)因为AM//BN，
所以∠ABN + ∠A = 180°，
所以∠ABN = 180° - 64° = 116°，
所以∠ABP + ∠PBN = 116°。
因为BC平分∠ABP，BD平分∠PBN，所以∠ABP = 2∠CBP，∠PBN = 2∠DBP，
所以2∠CBP + 2∠DBP = 116°，所以∠CBD = ∠CBP + ∠DBP = 58°。
(3)不变，∠APB:∠ADB = 2:1。理由如下:
因为AM//BN，
所以∠APB = ∠PBN，∠ADB = ∠DBN。
因为BD平分∠PBN，
所以∠PBD = ∠DBN，
所以∠PBD = ∠ADB，
所以∠PBN = 2∠ADB，
所以∠APB:∠ADB = 2:1。