《2025年畅行课堂七年级数学下册北师大版》

14. 已知xᵐ⁺ⁿ = 3，yᵐ⁺ⁿ = 2，求代数式−$\frac{1}{3}$xᵐyⁿ·(−$\frac{1}{2}$xⁿyᵐ)的值。

答案： 解:原式=[(−$\frac{1}{3}$)×(−$\frac{1}{2}$)]·x^(m + n)·y^(m + n)
　　　　　=$\frac{1}{6}$x^(m + n)y^(m + n)。
　因为x^(m + n)=3,y^(m + n)=2,
　所以原式=$\frac{1}{6}$×3×2=1。

15. 先化简，再求值：(−2a²b²)·(−ab²)² + ($\frac{1}{2}$a²b³)²·4b，其中a = 2，b = 1。

答案： 解:原式=−2a²b²·a²b²+$\frac{1}{4}$a⁴b⁶·4b
　　　　　=−2a⁴b⁴+a⁴b⁷
　当a = 2,b = 1时，
　原式=−2⁴×1⁴+2⁴×1⁷=−16 + 16 = 0。

16. 如图是篱笆围成的三块长方形菜地，已知FC = xm，DF = 2xm，FG = EG = 2.5xm。
(1)用含x的代数式表示AB，BC的长；
(2)用含x的代数式表示长方形ABCD的面积(要求化简)。

答案： 解:
(1)由题意,得AE = HG = DF = 2x m,FG = EG = 2.5x m,EB = FC = x m,
　所以AB = 2x + x = 3x(m),
　BC = EF = FG + EG = 5x(m)。
(2)S长方形ABCD = AB·BC = 3x·5x = 15x²(m²)。

17. [真实问题情境]如图，王老师把家里的WiFi密码设置成了数学问题。小明同学来王老师家做客，看到WiFi图片，思索了一会儿，输入密码，顺利地连接到了王老师家里的网络，那么他输入的密码是______________。

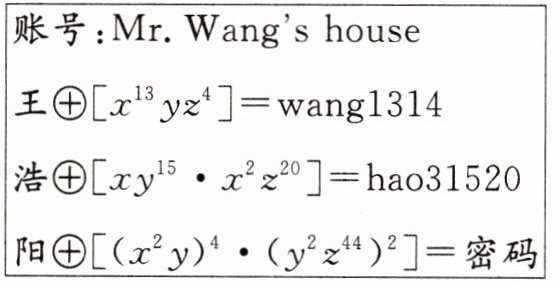
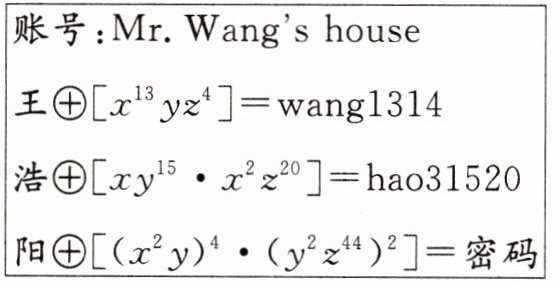
答案： yang8888