《2025年5年中考3年模拟七年级数学下册北京课改版》

1. (2024北京大兴期末)下列各式中，能用平方差公式进行因式分解的是(M7208002) ( )
A. x² + 1
B. x² - 4
C. x³ - 8
D. x² + 4x + 1

答案： B B.$x^{2}-4=(x + 2)(x - 2)$,能用平方差公式进行因式分解.故选 B.

2. (2023浙江丽水中考)分解因式x² - 9 = ________.(M7208002)

答案： 答案$(x + 3)(x - 3)$
解析$x^{2}-9=x^{2}-3^{2}=(x + 3)(x - 3).$

3. [教材变式](2024北京朝阳陈经纶中学一模)如果多项式ax² + by²只能因式分解为(3x + 2y)(3x - 2y)，则ab = ________.(M7208002)

答案： 答案 -36
解析 根据题意可得,$ax^{2}+by^{2}=(3x + 2y)(3x - 2y),$
$\therefore ax^{2}+by^{2}=9x^{2}-4y^{2},$
$\therefore a = 9,b = -4,$
$\therefore ab = 9×(-4)=-36.$

4. 分解因式:(M7208002)
(1) (2024陕西渭南白水期末)25 - 16x².
(2) (2024山东东营广饶期中)-x² + 4y².

答案： 解析
(1)$25 - 16x^{2}=5^{2}-(4x)^{2}=(5 + 4x)(5 - 4x).$
(2)$-x^{2}+4y^{2}=4y^{2}-x^{2}=(2y + x)(2y - x).$

5. [教材变式](2024湖南岳阳期中)下列各式中，不能用完全平方公式分解因式的是(M7208002) ( )
A. m² - m + 1/4
B. 16a² + 4a + 1
C. a² + 6ab + 9b²
D. a² + 2a + 1

答案： B A.$m^{2}-m+\frac{1}{4}=(m-\frac{1}{2})^{2}$;
B.$16a^{2}+4a + 1$不能用完全平方公式分解因式;
C.$a^{2}+6ab + 9b^{2}=(a + 3b)^{2}$;
D.$a^{2}+2a + 1=(a + 1)^{2}.$

6. (2024山东威海中考)因式分解(x + 2)(x + 4) + 1 = ________.(M7208002)

答案： 答案$(x + 3)^{2}$
解析 原式$=x^{2}+4x + 2x + 8 + 1$
$=x^{2}+6x + 9$
$=(x + 3)^{2}.$

7. [新独家原创]根据图示，写出一个多项式的因式分解过程:________________________.

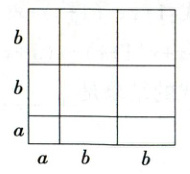
答案： 答案$a^{2}+4ab + 4b^{2}=(a + 2b)^{2}$
解析 从整体看,题图是边长为$(a + 2b)$的正方形,所以题图的面积为$(a + 2b)^{2}$;题图又可看成由 1 个边长为 a 的正方形,4 个长、宽分别为 b、a 的长方形,4 个边长为 b 的正方形组成的,所以题图的面积为$a^{2}+4ab + 4b^{2}$,因此可得$a^{2}+4ab + 4b^{2}=(a + 2b)^{2}.$

8. (2023北京东城文汇中学期末)分解因式:(M7208002)
(1) 4b² + 4b + 1.
(2) -x² + 2xy - y².

答案： 解析
(1)原式$=(2b)^{2}+2×2b×1 + 1^{2}$
$=(2b + 1)^{2}.$
(2)原式$=-(x^{2}-2xy + y^{2})$
$=-(x - y)^{2}.$

9. (2024云南中考)分解因式a³ - 9a = ( )
A. a(a - 3)(a + 3)
B. a(a² + 9)
C. (a - 3)(a + 3)
D. a²(a - 9)

答案： A 原式$=a(a^{2}-9)$
$=a(a - 3)(a + 3).$

10. (2024北京西城一模)分解因式x²y - 12xy + 36y = ________.(M7208002)

答案： 答案$y(x - 6)^{2}$
解析$x^{2}y-12xy + 36y=y(x^{2}-12x + 36)=y(x - 6)^{2}.$

11. (2023北京中考)分解因式x²y - y³ = ________.(M7208002)

答案： 答案$y(x + y)(x - y)$
解析$x^{2}y-y^{3}$
$=y(x^{2}-y^{2})$
$=y(x + y)(x - y).$

12. (2024北京北师大附中期中)因式分解:(M7208002)
(1) x³y - xy³.
(2) -2a²b + 16ab - 32b.

答案： 解析
(1)$x^{3}y-xy^{3}$
$=xy(x^{2}-y^{2})$
$=xy(x + y)(x - y).$
(2)$-2a^{2}b + 16ab-32b$
$=-2b(a^{2}-8a + 16)$
$=-2b(a - 4)^{2}.$

13. (2024北京交大附中期中,5,★☆☆)下列因式分解正确的是(M7208002) ( )
A. 4x² - 4xy + 1 = (2x + 1)²
B. x² - 25y² = (x - 25y)(x + 25y)
C. x² - 2xy = x(x - 2y)
D. x² + x - 2 = x(x + 1) - 2

答案： C A.$4x^{2}-4xy + 1$不能因式分解,故 A 选项错误;
B.$x^{2}-25y^{2}=(x - 5y)(x + 5y)$,故 B 选项错误;
C.$x^{2}-2xy=x(x - 2y)$,故 C 选项正确;
D.$x^{2}+x - 2=(x + 2)(x - 1)$,故 D 选项错误.

14. (2023河北中考,6,★☆☆)若k为任意整数，则(2k + 3)² - 4k²的值总能(M7208002) ( )
A. 被2整除
B. 被3整除
C. 被5整除
D. 被7整除

答案： B$(2k + 3)^{2}-4k^{2}$
$=(2k + 3-2k)(2k + 3 + 2k)$
$=3(4k + 3),$
$\because k$为任意整数,
$\therefore (2k + 3)^{2}-4k^{2}$的值总能被 3 整除.

15. (2024北京二中期末,15,★☆☆)已知4x² + kx + 9可以用完全平方公式进行因式分解，则k的值为 ________.(M7208002)

答案： 答案$\pm12$
解析$\because 4x^{2}+kx + 9$可以用完全平方公式进行因式分解,
$\therefore 4x^{2}+kx + 9=(2x)^{2}\pm12x + 3^{2}=(2x\pm3)^{2},$
$\therefore k=\pm12.$