2025年5年中考3年模拟七年级数学下册北京课改版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年中考3年模拟七年级数学下册北京课改版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. 下面使用类比推理恰当的是 ( )
A. “若a·3=b·3,则a=b”类比推出“若a·0=b·0,则a=b”
B. “(a+b)c=ac+bc”类比推出“(a·b)c=ac·bc”
C. “(a+b)c=ac+bc”类比推出“$\frac{a + b}{c}=\frac{a}{c}+\frac{b}{c}(c\neq0)$”
D. “(ab)^n=a^nb^n”类比推出“(a + b)^n=a^n + b^n”
A. “若a·3=b·3,则a=b”类比推出“若a·0=b·0,则a=b”
B. “(a+b)c=ac+bc”类比推出“(a·b)c=ac·bc”
C. “(a+b)c=ac+bc”类比推出“$\frac{a + b}{c}=\frac{a}{c}+\frac{b}{c}(c\neq0)$”
D. “(ab)^n=a^nb^n”类比推出“(a + b)^n=a^n + b^n”
答案:
C A.因为0乘任何数都等于0,所以A错误;B.类比推出的结果不符合乘法的运算性质,所以B错误;D.(1 + 1)²≠1² + 1²,所以D错误.由排除法可知选C.
2. 如图2,圆柱被一个平面斜切后得到一个几何体,类比梯形面积公式的推导方法(如图1)推导出图2中几何体的体积为________.(结果保留π)




答案:
答案 63π
解析 由题意可知几何体的体积为$\frac{1}{2}\times\pi(\frac{6}{2})^{2}\times(8 + 6)=63\pi$.
解析 由题意可知几何体的体积为$\frac{1}{2}\times\pi(\frac{6}{2})^{2}\times(8 + 6)=63\pi$.
3. 教材变式 (2024山东济南商河期末)如图所示:

(1)试验观察:
如果每过两点可以画一条直线,那么:
图①最多可以画________条直线;
图②最多可以画________条直线;
图③最多可以画________条直线.
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,那么最多可以画________条直线(用含n的代数式表示).
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握________次手.

(1)试验观察:
如果每过两点可以画一条直线,那么:
图①最多可以画________条直线;
图②最多可以画________条直线;
图③最多可以画________条直线.
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,那么最多可以画________条直线(用含n的代数式表示).
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握________次手.
答案:
答案
(1)3;6;10
(2)$\frac{n(n - 1)}{2}$
(3)990
解析
(1)如图所示:
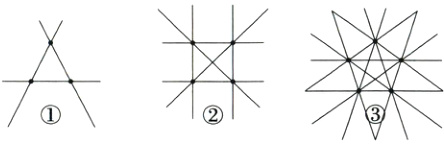
图①最多可以画3条直线;
图②最多可以画6条直线;
图③最多可以画10条直线.
(2)图①最多可以画3条直线,3 = 1 + 2;
图②最多可以画6条直线,6 = 1 + 2 + 3;
图③最多可以画10条直线,10 = 1 + 2 + 3 + 4;
……
如果平面上有n(n≥3)个点,且每3个点均不在同一条直线上,那么最多可以画1 + 2 + 3 + … + n - 1 = $\frac{n(n - 1)}{2}$条直线.
(3)$\frac{1}{2}\times45\times44 = 990$,共握990次手.
答案
(1)3;6;10
(2)$\frac{n(n - 1)}{2}$
(3)990
解析
(1)如图所示:

图①最多可以画3条直线;
图②最多可以画6条直线;
图③最多可以画10条直线.
(2)图①最多可以画3条直线,3 = 1 + 2;
图②最多可以画6条直线,6 = 1 + 2 + 3;
图③最多可以画10条直线,10 = 1 + 2 + 3 + 4;
……
如果平面上有n(n≥3)个点,且每3个点均不在同一条直线上,那么最多可以画1 + 2 + 3 + … + n - 1 = $\frac{n(n - 1)}{2}$条直线.
(3)$\frac{1}{2}\times45\times44 = 990$,共握990次手.
4. (2024北京十二中期中,19,★☆☆)如图,用围棋棋子按如图所示的规律摆图形,则摆第5个图形需要围棋棋子的枚数是________,第n个图形需要围棋棋子的枚数是________.


答案:
答案 29;6n - 1
解析 摆第1个图形需要围棋棋子的枚数是6×1 - 1 = 5;
摆第2个图形需要围棋棋子的枚数是6×2 - 1 = 11;
摆第3个图形需要围棋棋子的枚数是6×3 - 1 = 17;
摆第4个图形需要围棋棋子的枚数是6×4 - 1 = 23;
摆第5个图形需要围棋棋子的枚数是6×5 - 1 = 29;
……
∴摆第n个图形需要围棋棋子的枚数是6n - 1.
解析 摆第1个图形需要围棋棋子的枚数是6×1 - 1 = 5;
摆第2个图形需要围棋棋子的枚数是6×2 - 1 = 11;
摆第3个图形需要围棋棋子的枚数是6×3 - 1 = 17;
摆第4个图形需要围棋棋子的枚数是6×4 - 1 = 23;
摆第5个图形需要围棋棋子的枚数是6×5 - 1 = 29;
……
∴摆第n个图形需要围棋棋子的枚数是6n - 1.
5. (2024北京第一七一中学期中,18,★☆☆)a是不为1的有理数,我们把$\frac{1}{1 - a}$称为a的差倒数.例如:2的差倒数是$\frac{1}{1 - 2}=-1$, - 1的差倒数是$\frac{1}{1 - (-1)}=\frac{1}{2}$,已知$a_1=-\frac{1}{3}$,$a_2$是$a_1$的差倒数,$a_3$是$a_2$的差倒数,$a_4$是$a_3$的差倒数,……,则$a_4$=________,依此类推,$a_{2024}$=________.
答案:
答案 $-\frac{1}{3};\frac{3}{4}$
解析 由题意得$a_{1}=-\frac{1}{3}$,
$a_{2}=\frac{1}{1 - a_{1}}=\frac{1}{1 - (-\frac{1}{3})}=\frac{3}{4}$,
$a_{3}=\frac{1}{1 - a_{2}}=\frac{1}{1 - \frac{3}{4}} = 4$,
$a_{4}=\frac{1}{1 - a_{3}}=\frac{1}{1 - 4}=-\frac{1}{3}$,
……
∴这一列数按$-\frac{1}{3},\frac{3}{4},4$每3个数循环一次,
∵2024÷3 = 674……2,
∴$a_{2024}=a_{2}=\frac{3}{4}$.
解析 由题意得$a_{1}=-\frac{1}{3}$,
$a_{2}=\frac{1}{1 - a_{1}}=\frac{1}{1 - (-\frac{1}{3})}=\frac{3}{4}$,
$a_{3}=\frac{1}{1 - a_{2}}=\frac{1}{1 - \frac{3}{4}} = 4$,
$a_{4}=\frac{1}{1 - a_{3}}=\frac{1}{1 - 4}=-\frac{1}{3}$,
……
∴这一列数按$-\frac{1}{3},\frac{3}{4},4$每3个数循环一次,
∵2024÷3 = 674……2,
∴$a_{2024}=a_{2}=\frac{3}{4}$.
6. 推理能力 (2023浙江嘉兴中考)观察下面的等式:
$3^2 - 1^2=8×1$;$5^2 - 3^2=8×2$;$7^2 - 5^2=8×3$;$9^2 - 7^2=8×4$;…….
(1)写出$19^2 - 17^2$的结果.
(2)按上面的规律归纳出一个一般性结论(用含n的等式表示,n为正整数).
(3)请运用有关知识,推理说明(2)中的结论是正确的.
$3^2 - 1^2=8×1$;$5^2 - 3^2=8×2$;$7^2 - 5^2=8×3$;$9^2 - 7^2=8×4$;…….
(1)写出$19^2 - 17^2$的结果.
(2)按上面的规律归纳出一个一般性结论(用含n的等式表示,n为正整数).
(3)请运用有关知识,推理说明(2)中的结论是正确的.
答案:
解析
(1)
∵(17 + 1)÷2 = 9,
∴19² - 17² = 8×9 = 72.
(2)(2n + 1)² - (2n - 1)² = 8n.
(3)
∵(2n + 1)² - (2n - 1)² = [(2n + 1)+(2n - 1)][(2n + 1)-(2n - 1)]=(2n + 1 + 2n - 1)(2n + 1 - 2n + 1)=4n×2 = 8n,
∴(2n + 1)² - (2n - 1)² = 8n,
(2)中的结论正确.
(1)
∵(17 + 1)÷2 = 9,
∴19² - 17² = 8×9 = 72.
(2)(2n + 1)² - (2n - 1)² = 8n.
(3)
∵(2n + 1)² - (2n - 1)² = [(2n + 1)+(2n - 1)][(2n + 1)-(2n - 1)]=(2n + 1 + 2n - 1)(2n + 1 - 2n + 1)=4n×2 = 8n,
∴(2n + 1)² - (2n - 1)² = 8n,
(2)中的结论正确.
查看更多完整答案,请扫码查看


