《2025年5年中考3年模拟七年级数学下册北京课改版》

12. [跨物理·测体积]（2024山东聊城阳谷二模）测量玻璃球体积的过程如下：
步骤一：将180 cm³的水装进一个容量为300 cm³的杯子中；
步骤二：将三个相同的玻璃球放入水中，结果水没有满；
步骤三：再加入一个同样的玻璃球，结果水有溢出.
根据以上过程，请你推测一个玻璃球的体积x（cm³）的取值范围是__________.

答案： 答案 30＜x＜40
解析 由题意得$\begin{cases}3x＜300 - 180 \\4x＞300 - 180\end{cases}$，
解得30＜x＜40.

13. 已知不等式4x - 3a＞-1与不等式2(x - 1)+3＞5的解集相同，则a = ________.

答案： 答案 3
解析 解不等式4x - 3a＞ - 1得$x＞\frac{3a - 1}{4}$，解不等式2(x - 1)+3＞5得x＞2，
由题意得$\frac{3a - 1}{4}=2$，解得a = 3.

14. （2023广东中考）某商品进价为4元，标价为5元，商家准备打折销售，但其利润率不能少于10%，则最多可打________折.

答案： 答案 八八
解析 设这种商品可打x折销售，
由题意得5×0.1x - 4≥4×10%，
解得x≥8.8，
∴该商品最多可打八八折.

15. （2024北京十九中模拟）（5分）解不等式$\frac{1}{2}x - 1≤\frac{2}{3}x - \frac{1}{2}$，并把它的解集在数轴上表示出来.

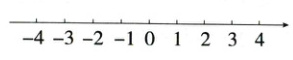
答案： 解析 去分母得3x - 6≤4x - 3，
移项得3x - 4x≤6 - 3，
合并同类项得 - x≤3，
系数化为1得x≥ - 3.
解集在数轴上表示如图.
−4−3−2−101234

16. （2022北京中考）（5分）解不等式组：$\begin{cases}2 + x＞7 - 4x \\ x＜\frac{4 + x}{2}\end{cases}$

答案： 解析 由2 + x＞7 - 4x，得x＞1，
由$x＜\frac{4 + x}{2}$，得x＜4，
则不等式组的解集为1＜x＜4.

17. （7分）黑板上有这样一道题，解不等式：$\frac{2x + 1}{3}≥\frac{x + 5}{2}+\square$.
学生：“老师，小聪把这道题后面的部分擦掉了.”
老师：“哦，如果我告诉你这道题的正确答案是x≥7，且后面的□代表一个常数，你能把这个常数补上吗？”
学生：“我知道了.”
根据以上信息，请你求出□代表的常数.

答案： 解析 设□代表的常数为a，则原不等式为$\frac{2x + 1}{3}\geq\frac{x + 5}{2}+a$，解这个不等式，得x≥13 + 6a，
因为这道题的正确答案是x≥7，所以13 + 6a = 7，解得a = - 1. 故□代表的常数为 - 1.

18. [新考向·新定义试题]（2024北京顺义牛栏山一中月考）（7分）定义一种新运算“a☆b”：当a≥b时，a☆b = a - b；当a＜b时，a☆b = a + b.
例如：3☆(-4)=3 - (-4)=7，(-6)☆3=-6 + 3=-3.
（1）填空：(-5)☆(-4)=________.
（2）若(3x - 2)☆(2 - x)=6，求x的值.
（3）若(2m + 1)☆(m - 2)＞2，求m的取值范围.

答案： 解析
(1) - 9.
详解：
∵ - 5＜ - 4，
∴( - 5)☆( - 4)= - 5+( - 4)= - 9.
(2)①当3x - 2≥2 - x，即x≥1时，
(3x - 2)☆(2 - x)=3x - 2 - (2 - x)=6.
解得x = 2.5＞1，符合题意；
②当3x - 2＜2 - x，即x＜1时，
(3x - 2)☆(2 - x)=3x - 2+(2 - x)=6.
解得x = 3＞1，不符合题意.
综上，x的值为2.5.
(3)①当2m + 1≥m - 2，即m≥ - 3时，
(2m + 1)☆(m - 2)=(2m + 1) - (m - 2)＞2，
∴m＞ - 1，此时m＞ - 1.
②当2m + 1＜m - 2，即m＜ - 3时，
(2m + 1)☆(m - 2)=(2m + 1)+(m - 2)＞2，
∴m＞1，此时无解.
综上，m的取值范围为m＞ - 1.