《2025年5年中考3年模拟七年级数学下册北京课改版》

1. （2023广东深圳龙华爱义学校期中）下列式子中不是不等式的是 （ ）
A. 5＜7
B. 2x＞3
C. $\frac{x - 1}{3}$＞1
D. 2a + 1 = 1

答案： 根据不等式的定义，可知5＜7，2x＞3，$\frac{x - 1}{3}＞1$是不等式，2a + 1 = 1不是不等式，故选D.

2. （2024北京西城回民学校期中）不等式x＞1的解集在数轴上表示正确的是 （ ）

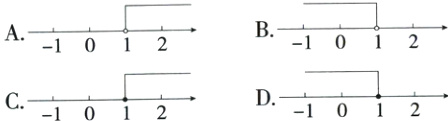
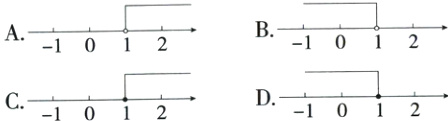
答案： 大于用空心圆圈，方向向右，故选A.

3. （2024北京二中期中）若a＞b，则下列不等式成立的是 （ ）
A. a²＞b²
B. -2a＞-2b
C. ac²＞bc²
D. a - b＞0

答案： 当a＞b时，$a^{2}＞b^{2}$不一定成立，故A不符合题意；
∵a＞b，
∴ - 2a＜ - 2b，故B不符合题意；当c≠0时，$ac^{2}＞bc^{2}$，当c = 0时，$ac^{2}=bc^{2}$，故C不符合题意；
∵a＞b，
∴a - b＞0，故D符合题意. 故选D.

4. （2024四川内江中考）不等式3x≥x - 4的解集是 （ ）
A. x≥-2
B. x≤-2
C. x＞-2
D. x＜-2

答案：
∵3x≥x - 4，
∴3x - x≥ - 4，
∴2x≥ - 4，
∴x≥ - 2.

5. （2024北京首都师大附中期中）不等式组$\begin{cases}x - 1＜1 \\ x≥-1\end{cases}$的解集在数轴上表示正确的是 （ ）

答案：
解不等式组得$\begin{cases}x＜2 \\x\geq - 1\end{cases}$，在数轴上表示为 ，故选B.

6. （2024北京师大附中一模）已知关于x的不等式3x + mx≥-4的解集在数轴上的表示如图所示，则m的值为 （ ）

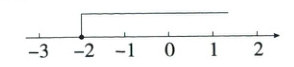
A. -$\frac{1}{2}$
B. -1
C. 1
D. $\frac{1}{2}$

答案：
∵3x + mx≥ - 4，
∴(3 + m)x≥ - 4，
观察数轴可知关于x的不等式3x + mx≥ - 4的解集是x≥ - 2，
∴$-\frac{4}{3 + m}=-2$，
∴6 + 2m = 4，解得m = - 1.

7. （2024山东青岛期中）王老师准备用60元购买钢笔和墨囊，已知一支钢笔5元，一盒墨囊8元，他购买了5支钢笔，则他最多还能购买墨囊 （ ）
A. 3盒
B. 4盒
C. 5盒
D. 6盒

答案： 设他还能购买x盒墨囊，
根据题意得5×5 + 8x≤60，
解得$x\leq4\frac{3}{8}$，因为x为整数，
所以他最多还能购买4盒墨囊.

8. （2024山东中考）根据以下对话，

给出下列三个结论：
①1班同学的最高身高为180 cm；
②1班同学的最低身高小于150 cm；
③2班同学的最高身高大于或等于170 cm.
上述结论中，所有正确结论的序号是 （ ）
A. ①②
B. ①③
C. ②③
D. ①②③

答案： 设1班同学的最高身高为x cm，最低身高为y cm，2班同学的最高身高为a cm，最低身高为b cm，
根据1班班长的对话，得x≤180，x + a = 350，
∴x = 350 - a，
∴350 - a≤180，解得a≥170，故③正确；
1班同学所有人的身高不超过180 cm，最高未必是180 cm，故①无法判断；根据2班班长的对话，得b＞140，y + b = 290，
∴b = 290 - y，
∴290 - y＞140，
∴y＜150，故②正确. 故选C.

9. [新考向·开放性试题]请写出一个解集为x＜-2的一元一次不等式组：________.

答案： 答案 $\begin{cases}x＜ - 2 \\x＜0\end{cases}$（答案不唯一）

10. （2024上海杨浦期中）当a________时，关于x的不等式ax - 1＞a - x的解集为x＜1.

答案： 答案 ＜ - 1
解析
∵ax - 1＞a - x，
∴(a + 1)x＞a + 1，
又
∵该不等式的解集为x＜1，
∴a + 1＜0，
∴a＜ - 1.

11. （2024北京西城期中）关于x的不等式组$\begin{cases}4x - 3≥2x - 5 \\ x + 2＜k + 6\end{cases}$有且只有3个整数解，则常数k的取值范围是__________.

答案： 答案 - 3＜k≤ - 2
解析 解不等式4x - 3≥2x - 5得x≥ - 1，
解不等式x + 2＜k + 6得x＜k + 4，
∵不等式组有且只有3个整数解，
∴不等式组的整数解为 - 1，0，1，
∴1＜k + 4≤2，解得 - 3＜k≤ - 2.