《2025年5年中考3年模拟七年级数学下册北京课改版》

21.(2024福建厦门大同中学期末)(10分)在数学课上,老师给出几个关于三位数的运算式子:
782 - 287=99×(7 - 2),876 - 678=99×(8 - 6),
986 - 689=99×(9 - 6),745 - 547=99×(7 - 5),
536 - 635=99×(5 - 6),…….
(1)张同学经过观察,提出一个猜想:把一个三位正整数的百位上的数与个位上的数交换位置,十位上的数不变,原数与所得数的差等于__________________________(请将他的猜想补充完整).
(2)张同学的猜想是否正确？若正确,请通过整式的运算进行证明;若不正确,说明理由.
(3)已知一个五位正整数的万位上的数为m,个位上的数为n,把万位上的数与个位上的数交换位置,其余数位上的数不变,原数与所得数的差等于__________________(用含m,n的式子表示).

答案： 解析
(1)99乘原数的百位上的数与个位上的数的差.
(2)张同学的猜想正确. 证明:设一个三位正整数的百位上的数为a,十位上的数为b,个位上的数为c,
∵ $100a + 10b + c-(100c + 10b + a)=100a + 10b + c - 100c - 10b - a = 99a - 99c$
=99(a−c),
　
∴张同学的猜想是正确的.
(3)9999(m−n).
　　详解:原数与所得数的差=10000m+n−(10000n+m)
　　=10000m+n−10000n−m
　　=9999m−9999n
　　=9999(m−n).

22.(2024北京中央民族大学附中期中)(10分)已知,线段AB,AD交于点A,C为直线AD上一点(不与点A,D重合).过点C在BC的右侧作射线CE⊥BC,过点D作直线DF//AB,交CE 于点G(G与D不重合).
(1)如图,若点C在线段AD上,且∠BCA为钝角.
①按要求补全图形.
②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系.
　　　　　　　　　　　

答案：

　22解析　
(1)①补全图形如图.
　　　　　　　
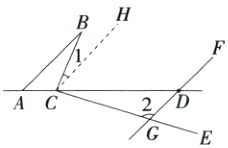
　　②∠CGD−∠B=90°.
　　证明:如图，过点C作CH//AB，
∴∠1=∠B.
　
∵AB//DF,
∴CH//DF:
　
∴∠2+∠HCG=180°.
　
∵CE⊥BC,
∴∠1+∠HCG=90°.
　
∴∠CGD+(90°−∠B)=180°,
　　即∠CGD−∠B=90°.
(2)∠CGD+∠B=90°.
　　详解:如图，过点C作CH//AB,
　　　　　　　
　
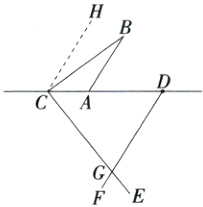
∴∠B=∠BCH,
　
∵AB//DF,
∴CH//DF,
　
∴∠CGD+∠HCG=180°,
　
∵CE⊥CB,
∴∠BCG=90°,
　
∴∠BCH+90°+∠CGD=180°,
　　即∠B+∠CGD=90°.