《2025年5年中考3年模拟七年级数学下册北京课改版》

11.(2024上海中考)计算(a + b)(b - a) =________.

答案： 答案 b^2 - a^2
解析 (a + b)(b - a) = (b + a)(b - a) = b^2 - a^2.

12.(2024北京海淀师达中学期中)若关于x的多项式(x^2 + 2x + 4)(x + k)展开后不含有x项,则有理数k的值为________.

答案： 答案 -2
解析 (x^2 + 2x + 4)(x + k)
= x^3 + 2x^2 + 4x + kx^2 + 2kx + 4k
= x^3 + (2 + k)x^2 + (4 + 2k)x + 4k，
∵展开后不含有x项，
∴4 + 2k = 0，解得k = -2.

13.(2024重庆西南大学附中期中)若3^m = 2,3^n = 5,则3^{2m - 3n} =________.

答案： 答案 4/125
解析 3^(2m - 3n) = 3^(2m)÷3^(3n) = (3^m)^2÷(3^n)^3 = 2^2÷5^3 = 4÷125 = 4/125.

14.(2022北京昌平一中期中)观察下列各式及其展开式:
(a + b)^2 = a^2 + 2ab + b^2;
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3;
(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4;
(a + b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5;
……
由此猜想(a + b)^10的展开式中第三项的系数是________.

答案： 答案 45
解析 (a + b)^2 = a^2 + 2ab + b^2;
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3;
(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4;
(a + b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5;
(a + b)^6 = a^6 + 6a^5b + 15a^4b^2 + 20a^3b^3 + 15a^2b^4 + 6ab^5 + b^6;
(a + b)^7 = a^7 + 7a^6b + 21a^5b^2 + 35a^4b^3 + 35a^3b^4 + 21a^2b^5 + 7ab^6 + b^7;
(a + b)^8的展开式的系数分别为1,8,28,56,70,56,28,8,1;
(a + b)^9的展开式的系数分别为1,9,36,84,126,126,84,36,9,1;
(a + b)^10的展开式的系数分别为1,10,45,120,210,252,210,120,45,10,1，
所以(a + b)^10的展开式中第三项的系数为45.

15.(6分)计算:
(1)[x^3y^5 + (-3x^4)^2]÷(-x^2).
(2)(x + y)(x^2 - xy + y^2).

答案： 解析
(1)原式 = (x^3y^5 + 9x^8)÷(-x^2) = -xy^5 - 9x^6.
(2)原式 = x^3 - x^2y + xy^2 + x^2y - xy^2 + y^3 = x^3 + y^3.

16.(6分)用乘法公式计算:
(1)100$\frac{1}{2}$×99$\frac{1}{2}$. (2)(20$\frac{1}{3}$)^2.

答案： 解析
(1)100 1/2×99 1/2 = (100 + 1/2)×(100 - 1/2) = 100^2 - (1/2)^2 = 9999 3/4.
(2)(20 1/3)^2 = (20 + 1/3)^2 = 20^2 + 2×20×1/3 + (1/3)^2 = 413 4/9.

17.(6分)
(1)已知x^2 - 2x - 1 = 0,求代数式2(x + 1)(x - 1) - (x + 1)^2的值.
(2)已知x + y = 4,xy = 2,求(x - y)^2的值.

答案： 解析
(1)原式 = 2(x^2 - 1) - (x^2 + 2x + 1)
= 2x^2 - 2 - x^2 - 2x - 1
= x^2 - 2x - 3.
∵x^2 - 2x - 1 = 0，
∴x^2 - 2x = 1，
∴原式 = x^2 - 2x - 3 = 1 - 3 = -2.
(2)(x - y)^2 = (x + y)^2 - 4xy
= 4^2 - 4×2
= 16 - 8
= 8.

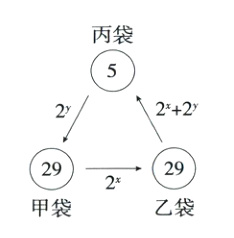
18.(2023江苏镇江中考改编)(6分)如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出2^x个球放入乙袋,再从乙袋中取出(2^x + 2^y)个球放入丙袋,最后从丙袋中取出2^y个球放入甲袋,此时三只袋中球的个数都相同,求2^{x + y}的值.
　　　　　

答案： 解析 由题意得5 - 2^y + 2^x + 2^y = 29 + 2^y - 2^x = 29 + 2^x - 2^x - 2^y，即5 + 2^x = 29 + 2^y - 2^x = 29 - 2^y，
∴{2×2^x - 2^y = 24, 2×2^y = 2^x}，解得{2^x = 16, 2^y = 8}，
∴2^(x + y) = 2^x×2^y = 16×8 = 128.

19.(8分)已知多项式$A = (x + 2)^2 + x(x - 2) - (x + 3)(x - 3).$
(1)化简多项式A时,小明的结果与其他同学的不同,请你检查小明同学的解题过程.
解$:A = (x + 2)^2 + x(x - 2) - (x + 3)(x - 3)$
$= x^2 + 2x + 4 + x^2 - 2x - x^2 - 9 = x^2 - 5.$
          ①                 ②            ③
在标出的①②③三项中,出现错误的是__________(填序号),请写出正确的解答过程.
(2)小亮说:“只要给出$x^2 + 2x + 1$的合理的值,即可求出多项式A的值.”小明给出$x^2 + 2x + 1$的值为4,请你求出此时A的值.

答案： 解析
(1)①③.解答过程$:A = (x + 2)^2 + x(x - 2) - (x + 3)(x - 3)$
$= x^2 + 4x + 4 + x^2 - 2x - x^2 + 9$
$= x^2 + 2x + 13.$
(2)
∵$x^2 + 2x + 1 = 4，$
∴$x^2 + 2x = 3，$
∴$A = x^2 + 2x + 13 = 3 + 13 = 16.$