《2025年5年中考3年模拟七年级数学下册北京课改版》

1.(2024江西九江都昌期中)计算(a - 2)(-a + 1)的结果是(M7206002) ( )
A.a² - a - 2 B.-a² - a - 2
C.-a² + 3a - 2 D.a² + 3a - 2

答案： C $(a - 2)(-a + 1)=-a^{2}+a + 2a - 2=-a^{2}+3a - 2$.

2.教材变式(2024北京首都师大附中期中)通过计算并比较图1,图2中阴影部分的面积,可以验证的式子是 ( )


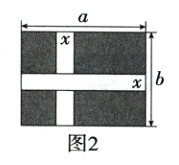
A.a(b - x)=ab - ax
B.b(a - x)=ab - bx
C.(a - x)(b - x)=ab - ax - bx
D.(a - x)(b - x)=ab - ax - bx + x²

答案： D 题图1中,阴影部分的面积$=(a - x)(b - x)$,题图2中,阴影部分的面积$=ab - ax - bx + x^{2}$,$\therefore(a - x)(b - x)=ab - ax - bx + x^{2}$.

3.(2024北京通州期中)已知(x + a)·(x + b)=x² + kx + ab,则k = ________.(用含有a,b的代数式表示)(M7206002)

答案： 答案 $a + b$
解析 $(x + a)(x + b)$
$=x^{2}+ax + bx + ab$
$=x^{2}+(a + b)x + ab$
$=x^{2}+kx + ab$,$\therefore k = a + b$.

4.计算:(M7206002)
(1)(2024北京东城广渠门中学期中)(5x + 2y)(3x - 2y).
(2)(2024北京昌平二中期中)(x + 3)(x - 2)+x(x + 1).

答案： 解析
(1)原式$=15x^{2}-10xy + 6xy - 4y^{2}$
$=15x^{2}-4xy - 4y^{2}$.
(2)原式$=x^{2}+x - 6 + x^{2}+x$
$=2x^{2}+2x - 6$.

5.如图,某公园计划在长为(3a + 4b)米,宽为(2a + 3b)米的长方形草地上修建横、纵各两条宽为a米的小路供行人散步,其余部分仍然为草地.
(1)求小路的面积.
(2)若a = 5,b = 12,求剩余草地的面积.

答案： 解析
(1)由题意可知剩余草地可以拼成一个长方形,且长为$3a + 4b - a - a=(a + 4b)$米,宽为$2a + 3b - a - a = 3b$(米),
$\therefore$剩余草地的面积为$(a + 4b)\cdot3b=(3ab + 12b^{2})$平方米,
$\therefore$小路的面积为$(3a + 4b)(2a + 3b)-(3ab + 12b^{2})$
$=6a^{2}+9ab + 8ab + 12b^{2}-3ab - 12b^{2}$
$=(6a^{2}+14ab)$平方米.
答:小路的面积为$(6a^{2}+14ab)$平方米.
(2)由
(1)可知剩余草地的面积为$(3ab + 12b^{2})$平方米,将$a = 5$,$b = 12$代入得,$3ab + 12b^{2}=3\times5\times12 + 12\times12^{2}=1908$.
答:剩余草地的面积为1908平方米.

6.(2024北京十三中期中,6,★☆☆)若2x + my与x - 2y的乘积的结果中不含xy项,则m的值为(M7206002) ( )
A.4 B.-4 C.2 D.-2

答案： A $(2x + my)\cdot(x - 2y)$
$=2x^{2}-4xy + mxy - 2my^{2}$
$=2x^{2}+(-4 + m)xy - 2my^{2}$,
$\because$结果中不含$xy$项,
$\therefore - 4 + m = 0$,
解得$m = 4$.故选A.

7.(2023北京通州期末,8,★☆☆)如图,有A类,B类两种正方形卡片和C类长方形卡片若干张,如果要拼一个长为(3a + b),宽为(a + 2b)的大长方形(要求:拼接的卡片无空隙、无重叠),那么需要C类卡片(M7206002) ( )

A.7张 B.6张 C.5张 D.4张

答案： A 大长方形的面积为$(3a + b)(a + 2b)=3a^{2}+3a\cdot2b + ba + 2b^{2}=3a^{2}+7ab + 2b^{2}$,
$\because A$类卡片的面积为$a^{2}$,$B$类卡片的面积为$b^{2}$,$C$类卡片的面积为$ab$,
$\therefore$需要$C$类卡片7张.故选A.

8.(2024北京首都师大附中期中,9,★☆☆)如图,在长为3a + 2,宽为2b - 1的长方形铁片上,挖去一个长为2a + 4,宽为b的小长方形铁片,则剩余部分的面积是(M7206002) ( )

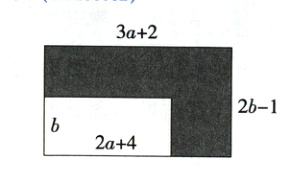
A.6ab - 3a + 4b B.4ab - 3a - 2
C.6ab - 3a + 8b - 2 D.4ab - 3a + 8b - 2

答案： B 剩余部分的面积为$(3a + 2)(2b - 1)-b(2a + 4)$
$=6ab - 3a + 4b - 2 - 2ab - 4b$
$=4ab - 3a - 2$.故选B.