《2025年5年中考3年模拟七年级数学下册北京课改版》

7. (2024北京一六一中学期中,8,)已知$a、b$为非零有理数,下面四个不等式组中,解集有可能为$-2＜x＜2$的不等式组是 ( )
A. $\begin{cases}ax＞1 \\bx＞1\end{cases}$
B. $\begin{cases}ax＜1 \\bx＜1\end{cases}$
C. $\begin{cases}ax＜1 \\bx＞1\end{cases}$
D. $\begin{cases}ax＞1 \\bx＜1\end{cases}$

答案： B 由题意得$\begin{cases}x＜2\\x＞-2\end{cases}$，
∴$\begin{cases}\frac{1}{2}x＜1\\-\frac{1}{2}x＜1\end{cases}$，
与四个选项中的不等式组比较可知，B选项的不等式组符合题意.

8. 跨体育与健康·跷跷板(2024北京海淀清华附中期中,8,)四个小朋友玩跷跷板的情况如图所示,他们的体重分别表示为$P,Q,R,S$,则$P,Q,R,S$大小关系是 ( )

A. $P＞R＞S＞Q$
B. $Q＞S＞P＞R$
C. $S＞P＞Q＞R$
D. $S＞P＞R＞Q$

答案： D 由题意得$\begin{cases}S＞P①\\P＞R②\\P + R＞Q + S③\end{cases}$，
由①得$Q + S＞Q + P$，代入③得$P + R＞Q + P$，所以$R＞Q$，
所以$P,Q,R,S$的大小关系为$S＞P＞R＞Q$.

9. (2024北京房山期中,10,)已知关于$x$的不等式组$\begin{cases}x＜2 \\x\geqslant m\end{cases}$,给出以下推断:
① 当$m = -3$时,不等式组的解集是$-3\leqslant x＜2$;
② 若不等式组的解集是$0\leqslant x＜2$,则$m = 0$;
③ 若不等式组无解,则$m\geqslant2$;
④ 若不等式组的整数解只有$-2,-1,0,1$,则$m = -2$.
其中所有正确推断的序号是 ( )
A. ①②③
B. ①②④
C. ①③④
D. ①②③④

答案： A ①当$m = - 3$时，不等式组的解集是$-3\leqslant x＜2$，故①正确；②若不等式组的解集是$0\leqslant x＜2$，则$m = 0$，故②正确；③若不等式组无解，则$m\geqslant2$，故③正确；④若不等式组的整数解只有$-2,-1,0,1$，则$-3＜m\leqslant - 2$，故④错误.故正确的有①②③，故选A.

10. (2024上海长宁期中,17,)已知关于$x$的不等式组$\begin{cases}x - 1＞2 \\x\leqslant m\end{cases}$无解,则$m$的取值范围是__________.(M7204003)

答案： 答案 $m\leqslant3$
解析 由不等式组可得$\begin{cases}x＞3\\x\leqslant m\end{cases}$，
因为原不等式组无解，所以$m\leqslant3$.

11. 教材变式(2024北京海淀清华附中期中,15,)已知关于$x$的不等式$2x - m＜1 - x$的正整数解是1,2,3,则$m$的取值范围是__________.

答案： 答案 $8＜m\leqslant11$
解析 $\because2x - m＜1 - x$，$\therefore2x + x＜m + 1$，
$\therefore3x＜m + 1$，$\therefore x＜\frac{m + 1}{3}$，
$\because$不等式的正整数解是$1,2,3$，$\therefore3＜\frac{m + 1}{3}\leqslant4$，
解得$8＜m\leqslant11$.

12. (2024北京东城广渠门中学期中,22,)解不等式组$\begin{cases}4(x + 1)\leqslant6x + 10 \\x - 3＜\frac{x - 8}{4}\end{cases}$并写出它的所有整数解.(M7204003)

答案： 解析 $\begin{cases}4(x + 1)\leqslant6x + 10①\\x - 3＜\frac{x - 8}{4}②\end{cases}$
解不等式①得$x\geqslant - 3$，
解不等式②得$x＜\frac{4}{3}$，
∴不等式组的解集为$-3\leqslant x＜\frac{4}{3}$，
∴不等式组的整数解为$-3,-2,-1,0,1$.

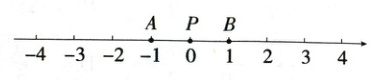
13. (2024北京十三中期中,24,)已知:如图,数轴上点$A、B$表示的数分别是 -1、1,点$P$在线段$AB$上,给出如下定义:如果在数轴上存在动点$Q$,满足$PQ = 2$,那么我们把这样的点$Q$表示的数称为联动数,特别地,当点$Q$表示的数是整数时我们称为联动整数.(M7204003)
(1) 在 -3,-1.5,0,2.5这四个数中,
① 若点$P$表示数0.5,则是联动数的有__________.
② 若点$P$是线段$AB$上任意一点,则可以是联动数的有__________.
(2) 关于$x$的方程$2x - m = x + 1$的解是联动数,求$m$的取值范围.
(3) 当不等式组$\begin{cases}\frac{x + 1}{2}＞-1 \\1 + 2(x - a)\leqslant3\end{cases}$的解集中恰好有4个联动整数时,求$a$的取值范围.
　　　　

答案： 解析
(1)①因为$0.5-(-3)=3.5$，$0.5-(-1.5)=2$，$0.5 - 0 = 0.5$，$2.5 - 0.5 = 2$，所以联动数的有$-1.5$，$2.5$.
②因为$-1-(-3)=2$，$0.5-(-1.5)=2$，$0-(-1)=1$，$1 - 0 = 1$，$2.5 - 0.5 = 2$，
所以可以是联动数的有$-3$，$-1.5$，$2.5$.
(2)解$2x - m = x + 1$得$x = m + 1$，
由题意得$\begin{cases}-1-m - 1\leqslant2\\1-m - 1\geqslant2\end{cases}$或$\begin{cases}m + 1-1\leqslant2\\m + 1+1\geqslant2\end{cases}$，
解得$-4\leqslant m\leqslant - 2$或$0\leqslant m\leqslant2$.
(3)$\begin{cases}\frac{x + 1}{2}＞-1①\\1 + 2(x - a)\leqslant3②\end{cases}$
解不等式①得$x＞-3$，
解不等式②得$x\leqslant a + 1$，
∵原不等式组的解集中恰好有4个联动整数，
∴四个联动整数为$-2$，$-1$，$1$，$2$，
∴$2\leqslant a + 1＜3$，$\therefore1\leqslant a＜2$，$\therefore a$的取值范围是$1\leqslant a＜2$.