2025年5年中考3年模拟七年级数学下册北京课改版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年中考3年模拟七年级数学下册北京课改版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7. (2024北京德胜中学期中,10,★★☆)观察下列图形中点的个数的规律,第7个图中点的个数是( )

A. 85
B. 51
C. 46
D. 64

A. 85
B. 51
C. 46
D. 64
答案:
A 第1个图中点的个数是4=$\frac{1×2}{2}$×3+1;
第2个图中点的个数是10=$\frac{2×3}{2}$×3+1;
第3个图中点的个数是19=$\frac{3×4}{2}$×3+1;
……
所以第n个图中点的个数为$\frac{3n(n + 1)}{2}$+1.
当n = 7时,$\frac{3n(n + 1)}{2}$+1=$\frac{3×7×8}{2}$+1 = 85,
即第7个图中点的个数为85.
第2个图中点的个数是10=$\frac{2×3}{2}$×3+1;
第3个图中点的个数是19=$\frac{3×4}{2}$×3+1;
……
所以第n个图中点的个数为$\frac{3n(n + 1)}{2}$+1.
当n = 7时,$\frac{3n(n + 1)}{2}$+1=$\frac{3×7×8}{2}$+1 = 85,
即第7个图中点的个数为85.
8. (2023湖北恩施州中考,16,★★☆)观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,…①
0,7,-4,21,-26,71,…②
根据你的发现,完成填空:
第①行数的第10个数为________;取每行数的第2023个数,则这两个数的和为________。
-2,4,-8,16,-32,64,…①
0,7,-4,21,-26,71,…②
根据你的发现,完成填空:
第①行数的第10个数为________;取每行数的第2023个数,则这两个数的和为________。
答案:
答案 1024;-2²⁰²⁴+2024
解析 观察这两行数可得,
第①行数的第10个数为(-2)¹⁰ = 1024,
第①行数的第2023个数为(-2)²⁰²³,
第②行数的第2023个数为(-2)²⁰²³+2024,
∵(-2)²⁰²³+(-2)²⁰²³+2024=-2²⁰²⁴+2024,
∴这两个数的和为-2²⁰²⁴+2024.
解析 观察这两行数可得,
第①行数的第10个数为(-2)¹⁰ = 1024,
第①行数的第2023个数为(-2)²⁰²³,
第②行数的第2023个数为(-2)²⁰²³+2024,
∵(-2)²⁰²³+(-2)²⁰²³+2024=-2²⁰²⁴+2024,
∴这两个数的和为-2²⁰²⁴+2024.
9. (2024北京八中期中,22,★★☆)下图中每一幅图都是由单位长度均为1的小正方形(包含白色小正方形和灰色小正方形)按某种规律组成的。
(1)根据规律,可得第4个图中共有________个小正方形,其中灰色小正方形共有________个。
(2)第n个图中,白色小正方形共有________个,灰色小正方形共有________个(用含n的式子表示,n为正整数)。
(3)白色小正方形可能比灰色小正方形的个数正好多64个吗?如果可能,求出n的值;如果不可能,请说明理由。


 ...
...
(1)根据规律,可得第4个图中共有________个小正方形,其中灰色小正方形共有________个。
(2)第n个图中,白色小正方形共有________个,灰色小正方形共有________个(用含n的式子表示,n为正整数)。
(3)白色小正方形可能比灰色小正方形的个数正好多64个吗?如果可能,求出n的值;如果不可能,请说明理由。


 ...
...
答案:
解析
(1)36;8.
详解:
∵第1个图中共有12 = 3×4个小正方形,其中灰色小正方形共有2个;
第2个图中共有20 = 5×4个小正方形,其中灰色小正方形共有2×2个;
第3个图中共有28 = 7×4个小正方形,其中灰色小正方形共有2×3个;
……
∴第n个图中共有4(2n + 1)个小正方形,其中灰色小正方形共有2n个,
∴第4个图中共有4×9 = 36个小正方形,其中灰色小正方形共有2×4 = 8个.
(2)(6n + 4);2n.
详解:由
(1)得,第n个图中,白色小正方形共有4(2n + 1)-2n=(6n + 4)个,灰色小正方形共有2n个.
(3)可能.由题意得2n+64 = 6n+4,解得n = 15.
(1)36;8.
详解:
∵第1个图中共有12 = 3×4个小正方形,其中灰色小正方形共有2个;
第2个图中共有20 = 5×4个小正方形,其中灰色小正方形共有2×2个;
第3个图中共有28 = 7×4个小正方形,其中灰色小正方形共有2×3个;
……
∴第n个图中共有4(2n + 1)个小正方形,其中灰色小正方形共有2n个,
∴第4个图中共有4×9 = 36个小正方形,其中灰色小正方形共有2×4 = 8个.
(2)(6n + 4);2n.
详解:由
(1)得,第n个图中,白色小正方形共有4(2n + 1)-2n=(6n + 4)个,灰色小正方形共有2n个.
(3)可能.由题意得2n+64 = 6n+4,解得n = 15.
10. 推理能力 (2024北京北师大附中月考)观察下列图形,寻找规律,回答下列问题。
定义数列:a₁,a₂,a₃,a₄,…,其中a₁ = a₂ = 1,aₖ + aₖ₊₁ = aₖ₊₂(k为任意正整数)。
如图,以数列中每一项的数为边长画出正方形,再将这些正方形按规律依次拼成长方形。
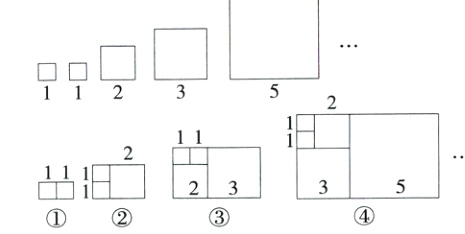
(1)按照图中的规律,图⑤中最大的长方形的周长为________。
(2)按照图中的规律,图⑨中最大的长方形的面积为________。
(3)从图中总结规律:求a₁² + a₂² + a₃² + … + a₁₀²的值。
定义数列:a₁,a₂,a₃,a₄,…,其中a₁ = a₂ = 1,aₖ + aₖ₊₁ = aₖ₊₂(k为任意正整数)。
如图,以数列中每一项的数为边长画出正方形,再将这些正方形按规律依次拼成长方形。

(1)按照图中的规律,图⑤中最大的长方形的周长为________。
(2)按照图中的规律,图⑨中最大的长方形的面积为________。
(3)从图中总结规律:求a₁² + a₂² + a₃² + … + a₁₀²的值。
答案:
解析
(1)42.
详解:图①中最大的长方形的周长为(1+2)×2 = 6;
图②中最大的长方形的周长为(2+3)×2 = 10;
图③中最大的长方形的周长为(3+5)×2 = 16;
图④中最大的长方形的周长为(5+8)×2 = 26;
所以图⑤中最大的长方形的周长为(8+13)×2 = 42.
(2)4895.
详解:易得图⑨中最大的长方形长为89,宽为55,
∴长方形的面积是89×55 = 4895.
(3)由
(2)得,$a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+\cdots +a_{10}^{2}$表示的是图⑨中最大的长方形的面积,
∴$a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+\cdots +a_{10}^{2}$=4895.
(1)42.
详解:图①中最大的长方形的周长为(1+2)×2 = 6;
图②中最大的长方形的周长为(2+3)×2 = 10;
图③中最大的长方形的周长为(3+5)×2 = 16;
图④中最大的长方形的周长为(5+8)×2 = 26;
所以图⑤中最大的长方形的周长为(8+13)×2 = 42.
(2)4895.
详解:易得图⑨中最大的长方形长为89,宽为55,
∴长方形的面积是89×55 = 4895.
(3)由
(2)得,$a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+\cdots +a_{10}^{2}$表示的是图⑨中最大的长方形的面积,
∴$a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+\cdots +a_{10}^{2}$=4895.
查看更多完整答案,请扫码查看


