《2025年5年中考3年模拟七年级数学下册北京课改版》

1. (2024云南中考)按一定规律排列的代数式：2x，3x²，4x³，5x⁴，6x⁵，…，第n个代数式是（ ）
A. 2xⁿ
B. (n - 1)xⁿ
C. nxⁿ⁺¹
D. (n + 1)xⁿ

答案： D 从单项式的系数来看，第n个代数式的系数为(n +1)，从单项式的次数来看，第n个代数式中x的指数为n，所以第n个代数式为(n+1)xⁿ，故选D.

2. 跨化学·烷烃 (2024重庆中考A卷)烷烃是一类由碳、氢元素组成的有机化合物质，下图是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子。第1种(如图①)有4个氢原子，第2种(如图②)有6个氢原子，第3种(如图③)有8个氢原子，……，按照这一规律，第10种化合物的分子结构模型中氢原子的个数是（ ）

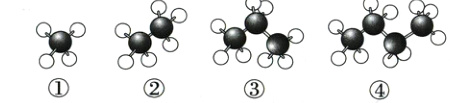
A. 20
B. 22
C. 24
D. 26

答案： B

3. 教材变式 (2024北京北师大附中期中)由一些点组成形如三角形的图形，前4个图形如图所示，则第n个图形中共有________个点。

答案： 答案 3n
解析 第1个图形中点的个数为3 = 1×3；
第2个图形中点的个数为6 = 2×3；
第3个图形中点的个数为9 = 3×3；
第4个图形中点的个数为12 = 4×3；
……
所以第n个图形中点的个数为3n.

4. 新独家原创 观察下面的图形：
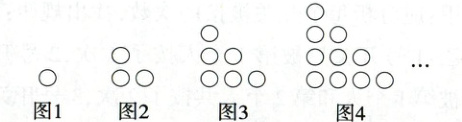
第1个图形由1个圆组成；第2个图形由3个圆组成；第3个图形由6个圆组成；第4个图形由10个圆组成；……。根据这个规律，推测第6个图形由________个圆组成，第n个图形由________个圆组成。

答案： 答案 21；$\frac{n(1 + n)}{2}$
解析 第1个图形中有1个圆；
第2个图形中有1+2 = 3个圆；
第3个图形中有1+2+3 = 6个圆；
第4个图形中有1+2+3+4 = 10个圆；
第5个图形中有1+2+3+4+5 = 15个圆；
第6个图形中有1+2+3+4+5+6 = 21个圆；
……
第n个图形中有1+2+3+4+…+n=$\frac{n(1 + n)}{2}$个圆. 故答案为21；$\frac{n(1 + n)}{2}$.

5. 新考向·规律探究题 (2024北京海淀清华附中期中)有一数值转换器，原理如图所示，若开始输入x的值是7，可发现第1次输出的结果是12；第2次输出的结果是6；……，那么第2023次输出的结果是________。

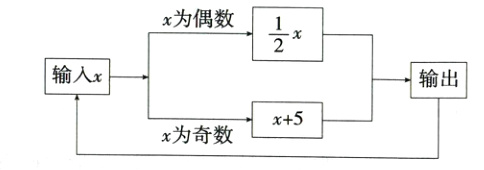
答案： 答案 1
解析 第1次输出的结果是12；第2次输出的结果是6；第3次输出的结果是3；第4次输出的结果是8；第5次输出的结果是4；第6次输出的结果是2；第7次输出的结果是1，第8次输出的结果是6；……
∴从第2次起，输出的结果按6，3，8，4，2，1循环，
∵(2023 - 1)÷6 = 337，
∴第2023次输出的结果是1.

6. (2022安徽中考)观察以下等式：
第1个等式：(2×1 + 1)²=(2×2 + 1)²-(2×2)²；
第2个等式：(2×2 + 1)²=(3×4 + 1)²-(3×4)²；
第3个等式：(2×3 + 1)²=(4×6 + 1)²-(4×6)²；
第4个等式：(2×4 + 1)²=(5×8 + 1)²-(5×8)²；
……
按照以上规律，解决下列问题：
(1)写出第5个等式：________________________。
(2)写出你猜想的第n个等式(用含n的式子表示)，并证明。

答案： 解析
(1)(2×5+1)²=(6×10+1)²-(6×10)².
(2)第n个等式：
(2n+1)²=[(n + 1)×2n+1]²-[(n + 1)×2n]².
证明：左边 = 4n²+4n+1，
右边 =[(n + 1)×2n]²+2×(n + 1)×2n+1²-[(n + 1)×2n]² = 4n²+4n+1，
∴左边 = 右边.
∴等式成立.