《2025年5年中考3年模拟七年级数学下册北京课改版》

10. 作差法(2024山东青岛大学附中期中,6,)已知M = 2x² + x - 6,N = x² + x - 7,则M、N的大小关系是(M7206002)　　　　　　　　　　(　　　)
A. M = N
B. M ＞ N
C. M ＜ N
D. 不能确定

答案： 10B M - N = 2x² + x - 6 - (x² + x - 7)
= 2x² + x - 6 - x² - x + 7
= x² + 1＞0，
∴M＞N.
方法归纳：作差法
若a - b＞0，则a＞b；若a - b = 0，则a = b；若a - b＜0，则a＜b. 反之也成立. 这种比较大小的方法称为作差法.

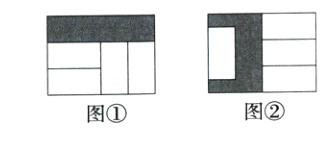
11. (2024北京通州期中,8,)两个形状、大小完全相同的长方形中分别放入4个相同的小长方形后,得到图①和图②中的阴影部分,如果大长方形的长为m,则图②与图①中的阴影部分周长之差是(M7206002)　　　　　　(　　　)

A. $-\frac{m}{2}$
B. $\frac{m}{2}$
C. $\frac{m}{3}$
D. $-\frac{m}{3}$

答案： 11B 设题图中小长方形的长为x，宽为y，大长方形的宽为n，
由题图得x + 2y = m，x = 2y，
∴y = 1/4m，
题图①中阴影部分的周长为2(n - 2y + m) = 2n - 4y + 2m，题图②中阴影部分的周长为2n + 2(m - x) + 2y = 2n + 6y，
∴题图②与题图①中的阴影部分周长之差是2n + 6y - (2n - 4y + 2m) = 10y - 2m = 5/2m - 2m = m/2.

12. (2024北京东城期末,17,)已知A = ax² - xy,
B = 2(x² - bxy) + y,a,b是常数,若A - B的差不含二次项,则ab = ________.(M7206001)

答案： 答案　1
解析 A - B
= ax² - xy - [2(x² - bxy) + y]
= ax² - xy - (2x² - 2bxy + y)
= ax² - xy - 2x² + 2bxy - y
= (a - 2)x² + (- 1 + 2b)xy - y，
∵A - B的差不含二次项，
∴a - 2 = 0， - 1 + 2b = 0，
解得a = 2，b = 1/2，
∴ab = 2×1/2 = 1.

13. 新考向.代数推理)(2024湖南长沙中考,16,)
某中学举办了一场庆祝活动,现场参与者均为在校中学生.其中有一个活动项目是“选数字猜出生年份”,该活动项目主持人要求参与者从1,2,3,4,5,6,7,8,9这九个数字中任取一个数字,先乘10,再加上4.6,将此时的运算结果再乘10,然后加上1978,最后减去参与者的出生年份(注:出生年份是一个四位数,比如2010年对应的四位数是2010),得到最终的运算结果.只要参与者报出最终的运算结果,主持人立马就知道参与者的出生年份.若某位参与者报出最终的运算结果是915,则这位参与者的出生年份是________.

答案： 答案　2009
解析 设选取的数字为x，出生年份为y. 依题意得，
10(10x + 4.6) + 1978 - y = 100x + 2024 - y = 915，
∴y = 1109 + 100x，
∵这位参与者为在校中学生，
∴出生时间应在2000年后，
∵100x表示一个三位数，
∴100x = 900，
∴y = 2009.

14. (2023北京北大附中期末,23,)已知代数式
A = 2x² + 3xy + 2y,B = x² - xy + x.(M7206002)
(1)求A - 2B.
(2)若A - 2B的值与x的取值无关,求y的值.

答案： 解析
(1)A - 2B = 2x² + 3xy + 2y - 2(x² - xy + x)
= 2x² + 3xy + 2y - 2x² + 2xy - 2x
= 5xy + 2y - 2x.
(2)A - 2B = 5xy + 2y - 2x = (5y - 2)x + 2y，
∵A - 2B的值与x的取值无关，
∴5y - 2 = 0，
解得y = 2/5.

15. 分类讨论思想(2024浙江杭州萧山一模,18,)
方方在做作业时,发现一道化简题目:3n - 4 - *·(n - 2)中有一个数字被墨水污染了(用*表示).(M7206002)
(1)如果被污染的数字是4,请计算正确的结果.
(2)如果化简的结果是单项式,那么被污染的数字是多少？

答案： 解析
(1)3n - 4 - 4(n - 2)
= 3n - 4 - 4n + 8
= - n + 4.
(2)设被污染的数字为k，
原式 = 3n - 4 - kn + 2k
= (3 - k)n + 2k - 4.
①若化简结果是不含有n的单项式，则3 - k = 0，解得k = 3，所以被污染的数字是3；
②若化简结果是含有n的单项式，则3 - k≠0，2k - 4 = 0，解得k = 2，所以被污染的数字是2.
综上，如果化简的结果是单项式，那么被污染的数字是3或2.