《2025年全优课堂九年级数学下册华师大版》

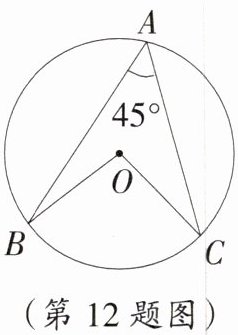
12. 如图，已知⊙O的半径为4，∠A = 45°，若一个圆锥的侧面展开图与扇形OBC能完全重合，则该圆锥的底面圆的半径为 ____________.

答案： 1 提示：$\because\angle A = 45^{\circ}$，$\therefore\angle BOC = 90^{\circ}$，$\therefore$ 扇形 $OBC$ 的弧长为 $\frac{90\pi\times4}{180}=2\pi$。设圆锥的底面圆半径为 $r$，则 $2\pi r = 2\pi$，解得 $r = 1$。

13. 在Rt△ABC中，∠C = 90°，AB = 13，BC = 5，以AC所在的直线为轴旋转一周，所得圆锥的全面积为 ______.

答案： $90\pi$ 提示：$\because$ 所得圆锥的底面圆半径为 $5$，母线长为 $13$，$\therefore$ 圆锥的侧面积为 $\pi\times5\times13 = 65\pi$，底面积为 $\pi\times5^2 = 25\pi$，$\therefore$ 全面积为 $65\pi+25\pi = 90\pi$。

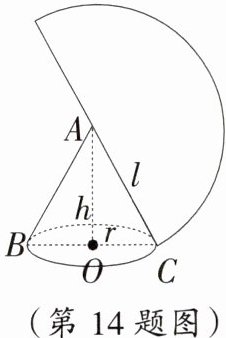
14. 如图，一个圆锥的高为3$\sqrt{3}$ cm，侧面展开图是半圆.求：
（1）圆锥的母线长与底面圆半径之比；
（2）∠BAC的度数；
（3）圆锥的侧面积.(结果保留π)

答案： 解：
(1)设此圆锥的高为 $h$，底面圆半径为 $r$，母线长 $AC = l$。$\because2\pi r=\pi l$，$\therefore\frac{l}{r}=2$，即圆锥的母线长与底面圆半径之比为 $2:1$；
(2)$\because\frac{l}{r}=2$，$\therefore$ 圆锥的高与母线的夹角为 $30^{\circ}$，则 $\angle BAC = 2\times30^{\circ}=60^{\circ}$；
(3)已知 $l^2 = h^2 + r^2$，$h = 3\sqrt{3}\text{ cm}$，$\therefore(2r)^2=(3\sqrt{3})^2 + r^2$，且 $r＞0$，$\therefore r = 3\text{ cm}$，$\therefore l = 2r = 6\text{ cm}$。$\therefore$ 圆锥的侧面积为 $\pi rl = 3\times6\times\pi = 18\pi(\text{cm}^2)$。

15. 蒙古包可近似地看作由圆锥和圆柱组成，现在准备用毛毡搭建一个底面圆面积为25π m²，圆柱高为3 m，圆锥高为2 m的蒙古包，求需要的毛毡面积.

答案： 解：设底面圆的半径为 $R$，则 $\pi R^2 = 25\pi$，所以 $R = 5$。由勾股定理得，圆锥的母线长 $=\sqrt{5^2 + 2^2}=\sqrt{29}$，所以圆锥的侧面积 $=\frac{1}{2}\times2\pi\times5\times\sqrt{29}=5\sqrt{29}\pi$；圆柱的侧面积 $=2\pi\times5\times3 = 30\pi$，所以需要毛毡的面积为 $(30\pi + 5\sqrt{29}\pi)\text{ m}^2$。

16. (东营中考)用一张半圆形铁皮，围成一个底面半径为4 cm的圆锥形工件的侧面(接缝忽略不计)，则圆锥的母线长为 （ ）
A. 4 cm
B. 8 cm
C. 12 cm
D. 16 cm

答案： B

17. (济宁中考)已知圆锥的母线长8 cm，底面圆的直径6 cm，则这个圆锥的侧面积是( )
A. 96π cm²
B. 48π cm²
C. 33π cm²
D. 24π cm²

答案： D

18. (邵阳中考)如图1，在等腰三角形ABC中，∠BAC = 120°，AD是∠BAC的平分线，且AD = 6，以点A为圆心，AD长为半径画$\overset{\frown}{EF}$，交AB于点E，交AC于点F.
（1）求由$\overset{\frown}{EF}$及线段FC，CB，BE围成图形(图1中阴影部分)的面积；
（2）将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，如图2，圆锥侧面无重叠，求这个圆锥的高$h$.

答案： 解：
(1)$\because$ 在等腰三角形 $ABC$ 中，$\angle BAC = 120^{\circ}$，$\therefore\angle B = 30^{\circ}$。$\because AD$ 是 $\angle BAC$ 的平分线，$\therefore AD\perp BC$，$BD = CD$，$\therefore BD=\sqrt{3}AD = 6\sqrt{3}$，$\therefore BC = 2BD = 12\sqrt{3}$，$\therefore$ 由 $\overset{\frown}{EF}$ 及线段 $FC$，$CB$，$BE$ 围成图形（图中阴影部分）的面积 $=S_{\triangle ABC}-S_{扇形 EAF}=\frac{1}{2}\times6\times12\sqrt{3}-\frac{120\cdot\pi\cdot6^2}{360}=36\sqrt{3}-12\pi$；
(2)设圆锥的底面圆的半径为 $r$，根据题意得 $2\pi r=\frac{120\cdot\pi\cdot6}{180}$，解得 $r = 2$，$\therefore$ 这个圆锥的高 $h=\sqrt{6^2 - 2^2}=4\sqrt{2}$。

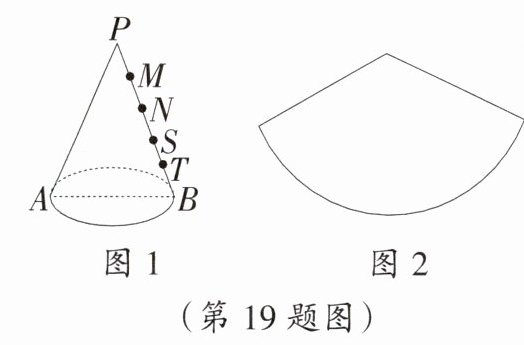
19. 已知AB是圆锥(如图1)底面的直径，P是圆锥的顶点，此圆锥的侧面展开图如图2所示.一只蚂蚁从A点出发，沿着圆锥侧面经过PB上一点，最后回到A点.若此蚂蚁所走的路线最短，那么M，N，S，T(M，N，S，T均在PB上)四个点中，它最有可能经过的点是 （ ）


A. M
B. N
C. S
D. T

答案：
B 提示：如图，根据圆锥侧面展开图，此蚂蚁所走的路线最短，那么 $M$，$N$，$S$，$T$（$M$，$N$，$S$，$T$ 均在 $PB$ 上）四个点中，它最有可能经过的点是 $N$。