《2025年全优课堂九年级数学下册华师大版》

8. 若一种服装的销售盈利y（万元）与销售数量x（万件）满足函数关系式y = - 2x² + 4x + 5，则盈利 （ ）
A. 最大值为5万元
B. 最大值为7万元
C. 最小值为5万元
D. 最小值为7万元

答案： B
提示:$y=-2x^2 + 4x + 5=-2(x^2 - 2x)+5=-2[(x - 1)^2 - 1]+5=-2(x - 1)^2 + 7$，则盈利最大值为$7$万元。

9. 如图，一边靠墙（墙有足够长），其他三边用12 m长的篱笆围成一个矩形（ABCD）花园，这个花园的最大面积是 （ ）

A. 16 m²
B. 12 m²
C. 18 m²
D. 以上都不对

答案： C
提示:设与矩形墙垂直的边的长度为$x m$，则这个花园的面积$S=x(12 - 2x)=-2x^2 + 12x=-2(x - 3)^2 + 18(m^2)$，
$\therefore$当$x = 3$时，$S$取得最大值，此时$S = 18$。

10. 某产品进货单价为90元，按每件100元出售，能售500件，若单价每涨1元，其销售量就减少10件，为了获得最大利润，其销售单价应定为 （ ）
A. 130元
B. 120元
C. 110元
D. 100元

答案： B
提示:设应涨价$x$元，则所获利润为$y=(100 + x - 90)(500 - 10x)=-10x^2 + 400x + 5000=-10(x - 20)^2 + 9000$，
可得涨价$20$元，即单价为$100 + 20 = 120$（元）时获利最大。

11. 用长度为2l的材料围成一个矩形场地，中间有2个隔墙，要使矩形的面积最大，则隔墙的长度为 （ ）
A. $\frac{l}{4}$
B. $\frac{l}{3}$
C. $\frac{l}{2}$
D. l

答案： A
提示:设隔墙的长为$x$，矩形面积为$y$，$y=x\times\frac{2l - 4x}{2}=x(l - 2x)=-2x^2 + lx$，
$\therefore$当$x=-\frac{b}{2a}=-\frac{l}{2\times(-2)}=\frac{l}{4}$时，$y$最大。

12. 某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件.市场调查反映：如果每件售价每涨1元（售价每件不能高于45元），那么每星期少卖10件.设每件售价为x元（x为非负整数），则若要使每星期的利润最大且每星期的销量较大，x应为 （ ）
A. 41
B. 42
C. 42.5
D. 43

答案： B
提示:由题意得，涨价$(x - 40)$元时，$(40\leqslant x\leqslant45$且$x$为整数$)$，每星期少卖$10(x - 40)$件，
$\therefore$每星期的销量为$150 - 10(x - 40)=550 - 10x$（件）。
设每星期的利润为$y$元，
则$y=(x - 30)(550 - 10x)=-10(x - 42.5)^2 + 1562.5$。
$\because40\leqslant x\leqslant45$且$x$为整数，$\therefore$当$x = 42$或$43$时，利润最大，为$1560$元。
又$\because$要求销量较大，$\therefore x$取$42$。
$\therefore$若要使每星期的利润最大且每星期的销量较大，$x$应为$42$。

13. 将进货单价为70元的某种商品按零售价100元售出时，每天能卖出20个.若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1个，为了获得最大利润，则应降价_____元，最大利润为_____元.

答案： 5 625
提示:设应降价$x$元，则销售量为$(20 + x)$个，根据题意得利润$y=(100 - x - 70)\times(20 + x)=-x^2 + 10x + 600=-(x - 5)^2 + 625$（元），
故为了获得最大利润，应降价$5$元，最大利润为$625$元。

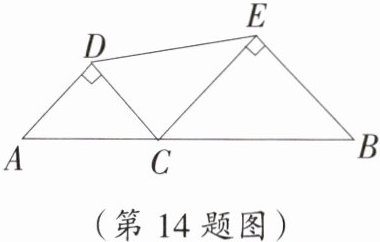
14. 如图，线段AB的长为2，C为AB上一个动点，分别以AC，BC为斜边在AB的同侧作等腰直角三角形ACD和等腰直角三角形BCE，连结DE，那么DE长的最小值是_____.

答案： 1
提示:设$AC = x$，则$BC = 2 - x$。
$\because\triangle ACD$和$\triangle BCE$都是等腰直角三角形，$\therefore\angle DCA = 45^{\circ}$，$\angle ECB = 45^{\circ}$，
可求得$DC^2=\frac{1}{2}x^2$，$CE^2=\frac{1}{2}(2 - x)^2$，$\angle DCE = 90^{\circ}$，
故$DE^2=DC^2 + CE^2=\frac{1}{2}x^2+\frac{1}{2}(2 - x)^2=x^2 - 2x + 2=(x - 1)^2 + 1$。
$\because0＜x＜2$，$\therefore$当$x = 1$时，$DE^2$取得最小值，$DE$也取得最小值，最小值为$1$。

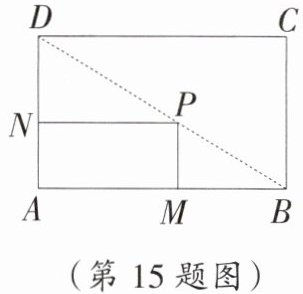
15. 如图，要在一矩形空地ABCD内建一个小矩形花坛AMPN，要求P在BD上，M，N分别在AB，AD上，已知AB = 160 m，AD = 100 m，设AN = x m.
（1）设AM = y m，求y与x之间的函数表达式；
（2）当AM，AN的长度分别是多少时，花坛AMPN的面积最大？求出最大面积.

答案： 解:
(1)$\because$四边形$AMPN$是矩形，
$\therefore PN// AB$，$NP = AM$，
$\therefore\triangle DNP\sim\triangle DAB$。$\therefore\frac{DN}{DA}=\frac{NP}{AB}$。
$\because AB = 160$，$AD = 100$，$AN = x$，$AM = NP = y$，
$\therefore\frac{100 - x}{100}=\frac{y}{160}$，化简得$y=-\frac{8}{5}x + 160$；
(2)设花坛$AMPN$的面积为$S m^2$，
则$S = xy=x(-\frac{8}{5}x + 160)=-\frac{8}{5}(x - 50)^2 + 4000$。
$\because-\frac{8}{5}＜0$，$\therefore$当$x = 50$时，$S$有最大值，$S_{最大值}=4000$。
即当$AM = 80 m$，$AN = 50 m$时，花坛$AMPN$面积最大，为$4000 m^2$。