《2025年全优课堂九年级数学下册华师大版》

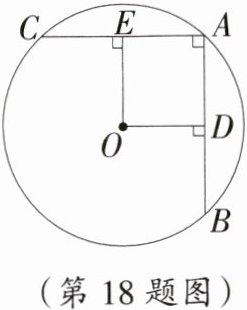
18. 如图，在⊙O中，AB，AC为互相垂直且相等的两条弦，OD⊥AB于点D，OE⊥AC于点E.
求证：四边形AEOD是正方形.

答案： 证明：
∵OD⊥AB，OE⊥AC，AB⊥AC，
∴∠OEA = ∠A = ∠ODA = 90°，
∴四边形AEOD为矩形.
∵OD⊥AB，
∴AD = BD = $\frac{1}{2}AB$.
同理AE = CE = $\frac{1}{2}AC$.
∵AB = AC，
∴AD = AE，
∴四边形AEOD是正方形.

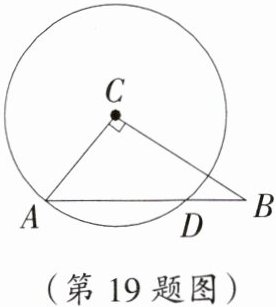
19. 如图，∠C=90°，以AC为半径的圆C与AB相交于点D.若AC=3，CB=4，求BD长.

答案：
解：
∵在三角形ABC中，∠ACB = 90°，AC = 3，BC = 4，
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$. 如图，过点C作CE⊥AB于点E，则AD = 2AE.
∵∠CAE = ∠CAB，∠AEC = ∠ACB = 90°，
∴△ACE∽△ABC，
∴$\frac{AC}{AB}=\frac{AE}{AC}$，
∴AC² = AE·AB，即3² = AE×5，
∴AE = 1.8，
∴AD = 2AE = 2×1.8 = 3.6，
∴BD = AB - AD = 5 - 3.6 = 1.4.

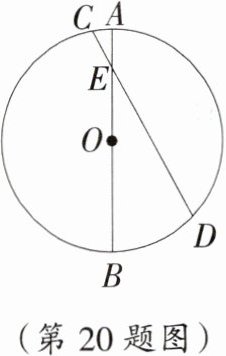
20. 如图，已知AB是⊙O的直径，弦CD交AB于点E，∠CEA =30°，OE=4，DE=5$\sqrt{3}$，求弦CD及⊙O的半径长.

答案：
解：如图，过点O作OM⊥CD于点M，连结OD.
∵∠CEA = 30°，
∴∠OEM = ∠CEA = 30°. 在Rt△OEM中，
∵OE = 4，
∴OM = $\frac{1}{2}OE = 2$，EM = OE·cos30° = 4×$\frac{\sqrt{3}}{2}=2\sqrt{3}$.
∵DE = 5$\sqrt{3}$，
∴DM = DE - EM = 3$\sqrt{3}$.
∵OM过圆心，OM⊥CD，
∴CD = 2DM，
∴CD = 6$\sqrt{3}$.
∵OM = 2，DM = 3$\sqrt{3}$，
∴在Rt△DOM中，OD = $\sqrt{OM^{2}+DM^{2}}=\sqrt{2^{2}+(3\sqrt{3})^{2}}=\sqrt{31}$，
∴弦CD的长为6$\sqrt{3}$，⊙O的半径长为$\sqrt{31}$.

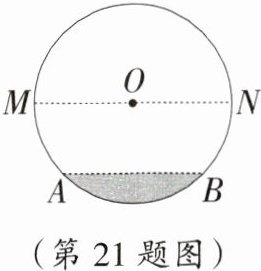
21. 在圆柱形油槽内装有一些油，油槽直径MN为10 dm.截面如图所示，油面宽AB为6 dm，如果再注入一些油后，油面宽变为8 dm，求油面AB上升的高度.

答案：
解：如图，连结OA，作OG⊥AB于点G，则AG = $\frac{1}{2}AB = 3$ dm. 因为OA = 5dm，根据勾股定理得OG = 4 dm，即弦AB的弦心距是4 dm. 同理当油面宽变为8 dm时，弦心距是3 dm，当油面没超过圆心O时，油上升了1 dm；当油面超过圆心O时，油上升了7 dm.
∴油面上升了1 dm或7 dm.

22.（黄冈中考）如图，一条公路的转弯处是一段圆弧（$\overset{\frown}{AB}$），点O是这段弧所在圆的圆心，AB =40 m，点C是$\overset{\frown}{AB}$的中点，点D是AB的中点，且CD=10 m，则这段弯路所在圆的半径为（ ）

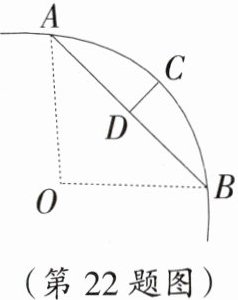
A. 25 m
B. 24 m
C. 30 m
D. 60 m

答案： A 提示：在题图上连结OC，
∵点C是$\overset{\frown}{AB}$的中点，
∴OC垂直平分AB.
∵D是AB的中点，
∴D在OC上，
∴AD = DB = 20 m，OD + CD = OC.
∴在Rt△AOD中，OA² = OD² + AD². 设半径为r，得r²=(r - 10)² + 20²，解得r = 25，即这段弯路所在圆的半径是25 m.

23.（荆门中考）如图，CD是圆O的弦，直径AB⊥CD，垂足为点E，若AB=12，BE=3，则四边形ACBD的面积为（ ）

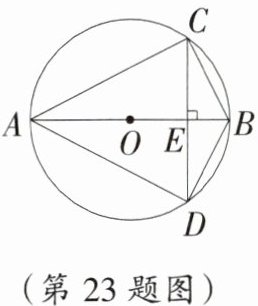
A. 36$\sqrt{3}$
B. 24$\sqrt{3}$
C. 18$\sqrt{3}$
D. 72$\sqrt{3}$

答案： A 提示：在题图上连结OC，
∵AB = 12，BE = 3，
∴OB = OC = 6，OE = 3，
∵AB⊥CD，在Rt△COE中，
EC = $\sqrt{OC^{2}-OE^{2}}=\sqrt{36 - 9}=3\sqrt{3}$，
∴CD = 2CE = 6$\sqrt{3}$，
∴四边形ACBD的面积 = $\frac{1}{2}AB·CD=\frac{1}{2}×12×6\sqrt{3}=36\sqrt{3}$.

24.（青海中考）如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分，如果C是⊙O中弦AB的中点，CD经过圆心O交⊙O于点D，并且AB=4 m，CD=6 m，则⊙O的半径为______ m.

答案： $\frac{10}{3}$ 提示：在题图上连结OA，设⊙O的半径为r m.
∵C是⊙O中弦AB的中点，CD过圆心，
∴CD⊥AB，AC = BC = $\frac{1}{2}AB = 2$ m. 在Rt△AOC中，
∵OA = r m，则OC=(6 - r) m，
∴2²+(6 - r)² = r²，解得r = $\frac{10}{3}$，即⊙O的半径长为$\frac{10}{3}$ m.

25. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长六寸，问径几何？”用现代的数学语言表述是：“CD为⊙O的直径，弦AB⊥CD，垂足为E，CE=1寸，AB=6寸，求直径CD的长.”依题意得CD的长为（寸：古代长度单位）（ ）

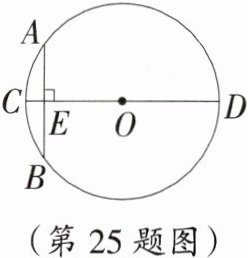
A. 4寸
B. 5寸
C. 8寸
D. 10寸

答案：
D 提示：如图，连结OA，设直径CD的长为2x寸，则半径OC = x寸.
∵CD为⊙O的直径，弦AB⊥CD于点E，AB = 6寸，
∴AE = BE = $\frac{1}{2}AB=\frac{1}{2}×6 = 3$(寸).
∵OA = x寸，CE = 1寸，根据勾股定理得x² = 3²+(x - 1)²，解得x = 5，
∴CD = 2x = 2×5 = 10(寸).