《2025年全优课堂九年级数学下册华师大版》

1. 到圆心的距离大于半径的点的集合是(　　　)
A. 圆的内部
B. 圆
C. 圆的外部
D. 圆的外部和圆

答案： C

2. 如图，AB是⊙O的直径，BC是⊙O的弦.若∠OBC=60°，则∠BAC的度数是(　　　)

A. 75°
B. 60°
C. 45°
D. 30°

答案： D

3. 已知⊙O的直径AB=6cm，则圆上任意一点到圆心的距离等于(　　　)
A. 2cm
B. 2.5cm
C. 3cm
D. 无法确定

答案： C

4. 如图，已知EF是⊙O的直径，把∠A为60°的三角板ABC的一条直角边BC放在直线EF上，斜边AB交⊙O于点P，点B与点O重合，且AC大于OE，将三角板ABC沿OE向左平移，到点B与点E重合为止.设∠POF=x°，则x的取值范围是(　　　)

A. 30≤x≤60
B. 30≤x≤90
C. 30≤x≤120
D. 60≤x≤120

答案： A

5. 如图，已知⊙O的直径CD为6，且CD⊥AB，∠D=15°，则OE的长为(　　　)

A. $\frac{3\sqrt{3}}{2}$
B. $3\sqrt{3}$
C. $\frac{3}{2}$
D. 3

答案： A

6. 如图，小明同学将汽车轮胎放置在地面台阶直角处，他测量了台阶高a为160mm，直角顶点到轮胎与底面接触点AB长为320mm，请帮小明计算轮胎的直径为(　　　)

A. 350mm
B. 700mm
C. 800mm
D. 400mm

答案： C 提示：在题图上连结OB，OC，作CD⊥OB于点D.设⊙O半径为x mm，在Rt△OCD中，由勾股定理得(x - 160)²+320²=x²，解得x = 400，
∴2x = 800.

7. 如图，在△ABC中，∠BAC=50°，把△ABC沿EF折叠，C的对应点恰好与圆心O(O为过A，B，C三点的圆的圆心)重合，则∠CFE的度数是(　　　)

A. 40°
B. 45°
C. 50°
D. 55°

答案： C 提示：在题图上连结OB，OC.由圆周角定理得∠BOC = 2∠BAC = 100°.
∵OB = OC，
∴∠OCF = $\frac{1}{2}$×(180° - 100°)=40°.由折叠的性质得OC⊥EF，
∴∠CFE = 90° - 40° = 50°.

8. 数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a.小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是__________________________.

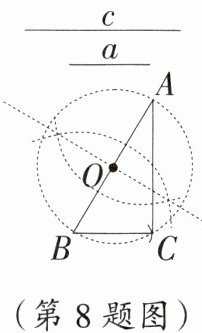
答案： 直径所对的圆周角是直角

9. 如图，⊙O中，弦AB长等于半径，则劣弧AB所对的圆心角度数是______.

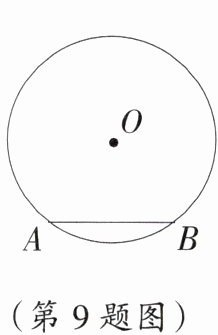
答案：
60° 提示：如图，连结OA，OB.
∵在⊙O中，弦AB的长等于半径，
∴OA = AB = OB，
∴△OAB是等边三角形，
∴∠AOB = 60°，
∴劣弧AB所对的圆心角度数是60°.

10. 如图，⊙O的直径AB过弦CD的中点E，若∠C=25°，则∠D=________.

答案： 65° 提示：
∵∠C = 25°，
∴∠A = ∠C = 25°.
∵⊙O的直径AB过弦CD的中点E，
∴AB⊥CD，
∴∠AED = 90°，
∴∠D = 90° - ∠A = 90° - 25° = 65°.

11. 如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，则∠B+∠E=______°.

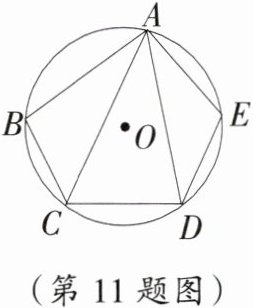
答案：
215 提示：如图，连结CE.
∵五边形ABCDE是圆内接五边形，
∴四边形ABCE是圆内接四边形，
∴∠B + ∠AEC = 180°.
∵∠CED = ∠CAD = 35°，
∴∠B + ∠AED = ∠B + ∠AEC + ∠CED = 180°+35° = 215°.