《2026年长江作业本同步练习册九年级数学下册人教版》

11. 求下列各式的值：
（1）$ \sin 45^{\circ} · \cos 45^{\circ} + \tan 60^{\circ} · \sin 60^{\circ} $；
（2）$ \sin 30^{\circ} - \tan^{2} 45^{\circ} + \dfrac{3}{4} \tan^{2} 30^{\circ} - \cos 60^{\circ} $.

答案： 11.
(1)2
(2)$ -\dfrac{3}{4} $

12. 在 $ \mathrm{Rt} △ ABC $ 中，$ ∠ C = 90^{\circ} $，$ AC = \sqrt{2} $，$ BC = \sqrt{6} $，解这个直角三角形.

答案： 12. $ A B=2 \sqrt{2}, ∠ A=60^{\circ}, ∠ B=30^{\circ} $.

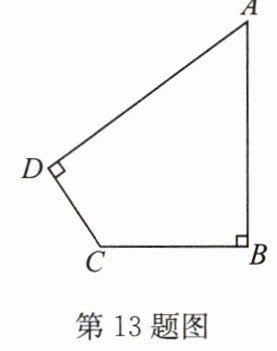
13. 如图，在四边形 $ ABCD $ 中，$ ∠ B = ∠ D = 90^{\circ} $，$ AB = 3 $，$ BC = 2 $，$ \tan A = \dfrac{4}{3} $，求 $ CD $ 的值.

答案： 13. $ C D=\dfrac{6}{5} $

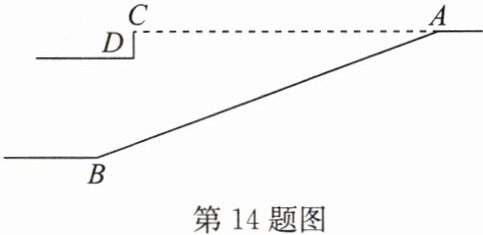
14. 随着私家车的增多，“停车难”成了很多小区的棘手问题.某小区为解决这个问题，拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图，其中，入口处斜坡 $ AB $ 的坡角为 $ 20^{\circ} $，水平线 $ AC = 12 \, \mathrm{m} $，$ CD ⊥ AC $，$ CD = 1.5 \, \mathrm{m} $.根据规定，地下停车库坡道入口上方要张贴限高标志，以提醒驾驶员所驾的车辆能否安全驶入.请求出限制高度为多少米.（结果精确到 $ 0.1 \, \mathrm{m} $，参考数据：$ \sin 20^{\circ} \approx 0.34 $，$ \cos 20^{\circ} \approx 0.94 $，$ \tan 20^{\circ} \approx 0.36 $）

答案： 14. 限制高度约为 2.6 米

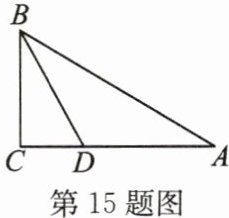
15. 如图，在 $ △ ABC $ 中，$ ∠ C = 90^{\circ} $，$ \tan A = \dfrac{\sqrt{3}}{3} $，$ ∠ ABC $ 的平分线 $ BD $ 交 $ AC $ 于点 $ D $，$ CD = \sqrt{3} $，求 $ AB $ 的长.

答案： 15. 6