第68页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
三、解答题
14. 如图,已知$\odot O$的弦$CD$垂直于直径$AB$,点$E$在$CD$上,且$EC = EB$.
(1) 求证:$△ CEB∽△ CBD$;
(2) 若$CE = 3$,$CB = 5$,求$DE$的长.
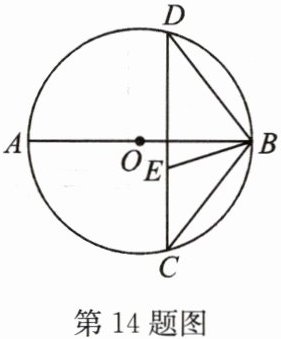
14. 如图,已知$\odot O$的弦$CD$垂直于直径$AB$,点$E$在$CD$上,且$EC = EB$.
(1) 求证:$△ CEB∽△ CBD$;
(2) 若$CE = 3$,$CB = 5$,求$DE$的长.

答案:
14.
(1)略
(2)$5\frac{1}{3}$
(1)略
(2)$5\frac{1}{3}$
15. 如图,在$△ ABC$中,$AB = AC = 1$,$BC=\frac{\sqrt{5}-1}{2}$,在$AC$上取一点$D$,使得$AD = BC$,连$BD$.
(1) 求证:$AD^{2}=AC· CD$;
(2) 求$∠ ABD$的度数.
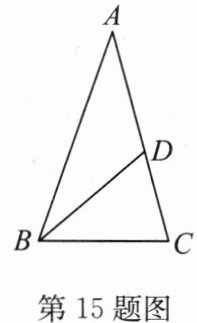
(1) 求证:$AD^{2}=AC· CD$;
(2) 求$∠ ABD$的度数.

答案:
1. (1)证明:
已知$AB = AC = 1$,$BC = AD=\frac{\sqrt{5}-1}{2}$,则$CD=AC - AD=1-\frac{\sqrt{5}-1}{2}=\frac{2 - (\sqrt{5}-1)}{2}=\frac{3 - \sqrt{5}}{2}$。
计算$AD^{2}$:$AD^{2}=(\frac{\sqrt{5}-1}{2})^{2}=\frac{5 - 2\sqrt{5}+1}{4}=\frac{6 - 2\sqrt{5}}{4}$。
计算$AC· CD$:$AC· CD = 1×\frac{3 - \sqrt{5}}{2}=\frac{3 - \sqrt{5}}{2}$,又$\frac{AD^{2}}{AC· CD}=\frac{(\frac{\sqrt{5}-1}{2})^{2}}{1×\frac{3 - \sqrt{5}}{2}}=\frac{\frac{5 - 2\sqrt{5}+1}{4}}{\frac{3 - \sqrt{5}}{2}}=\frac{6 - 2\sqrt{5}}{2(3 - \sqrt{5})}$。
对$\frac{6 - 2\sqrt{5}}{2(3 - \sqrt{5})}$进行化简:
分子分母同时乘以$3+\sqrt{5}$,$\frac{(6 - 2\sqrt{5})(3+\sqrt{5})}{2(3 - \sqrt{5})(3+\sqrt{5})}$。
根据$(a + b)(a - b)=a^{2}-b^{2}$,$(3 - \sqrt{5})(3+\sqrt{5})=9 - 5 = 4$;$(6 - 2\sqrt{5})(3+\sqrt{5})=18+6\sqrt{5}-6\sqrt{5}-10 = 8$。
所以$\frac{(6 - 2\sqrt{5})(3+\sqrt{5})}{2(3 - \sqrt{5})(3+\sqrt{5})}=\frac{8}{2×4}=1$,即$AD^{2}=AC· CD$。
2. (2)
因为$AD^{2}=AC· CD$,所以$\frac{AD}{AC}=\frac{CD}{AD}$,又$∠ A=∠ A$,根据相似三角形的判定定理(两边对应成比例且夹角相等的两个三角形相似),可得$△ ABD∼△ ACB$。
所以$\frac{AB}{AC}=\frac{BD}{CB}$,因为$AB = AC$,所以$BD = BC$。
设$∠ A=α$,因为$△ ABD∼△ ACB$,所以$∠ ABD=∠ C$。
又因为$AB = AC$,所以$∠ ABC=∠ C$。
根据三角形内角和定理$∠ A+∠ ABC+∠ C = 180^{\circ}$,即$α + 2∠ C=180^{\circ}$。
由$△ ABD∼△ ACB$,$\frac{AD}{AB}=\frac{AB}{AC}$($AB = AC$),$\cos A=\frac{AD^{2}+AC^{2}-CD^{2}}{2AD· AC}$,由$AD^{2}=AC· CD$,$AC = 1$,$AD=\frac{\sqrt{5}-1}{2}$,$CD=\frac{3 - \sqrt{5}}{2}$。
$\cos A=\frac{(\frac{\sqrt{5}-1}{2})^{2}+1^{2}-(\frac{3 - \sqrt{5}}{2})^{2}}{2×\frac{\sqrt{5}-1}{2}×1}$
先计算分子:$(\frac{\sqrt{5}-1}{2})^{2}+1-(\frac{3 - \sqrt{5}}{2})^{2}=\frac{5 - 2\sqrt{5}+1}{4}+1-\frac{9 - 6\sqrt{5}+5}{4}=\frac{6 - 2\sqrt{5}+4-(14 - 6\sqrt{5})}{4}=\frac{10 - 2\sqrt{5}-14 + 6\sqrt{5}}{4}=\frac{4\sqrt{5}-4}{4}=\sqrt{5}-1$。
分母$=\sqrt{5}-1$,所以$\cos A=\frac{\sqrt{5}-1}{2}$,则$∠ A = 36^{\circ}$。
因为$∠ A+∠ ABC+∠ C = 180^{\circ}$,$∠ ABC=∠ C$,所以$∠ C=∠ ABD = 72^{\circ}$。
综上,(1)证明过程如上述;(2)$∠ ABD = 36^{\circ}$。
已知$AB = AC = 1$,$BC = AD=\frac{\sqrt{5}-1}{2}$,则$CD=AC - AD=1-\frac{\sqrt{5}-1}{2}=\frac{2 - (\sqrt{5}-1)}{2}=\frac{3 - \sqrt{5}}{2}$。
计算$AD^{2}$:$AD^{2}=(\frac{\sqrt{5}-1}{2})^{2}=\frac{5 - 2\sqrt{5}+1}{4}=\frac{6 - 2\sqrt{5}}{4}$。
计算$AC· CD$:$AC· CD = 1×\frac{3 - \sqrt{5}}{2}=\frac{3 - \sqrt{5}}{2}$,又$\frac{AD^{2}}{AC· CD}=\frac{(\frac{\sqrt{5}-1}{2})^{2}}{1×\frac{3 - \sqrt{5}}{2}}=\frac{\frac{5 - 2\sqrt{5}+1}{4}}{\frac{3 - \sqrt{5}}{2}}=\frac{6 - 2\sqrt{5}}{2(3 - \sqrt{5})}$。
对$\frac{6 - 2\sqrt{5}}{2(3 - \sqrt{5})}$进行化简:
分子分母同时乘以$3+\sqrt{5}$,$\frac{(6 - 2\sqrt{5})(3+\sqrt{5})}{2(3 - \sqrt{5})(3+\sqrt{5})}$。
根据$(a + b)(a - b)=a^{2}-b^{2}$,$(3 - \sqrt{5})(3+\sqrt{5})=9 - 5 = 4$;$(6 - 2\sqrt{5})(3+\sqrt{5})=18+6\sqrt{5}-6\sqrt{5}-10 = 8$。
所以$\frac{(6 - 2\sqrt{5})(3+\sqrt{5})}{2(3 - \sqrt{5})(3+\sqrt{5})}=\frac{8}{2×4}=1$,即$AD^{2}=AC· CD$。
2. (2)
因为$AD^{2}=AC· CD$,所以$\frac{AD}{AC}=\frac{CD}{AD}$,又$∠ A=∠ A$,根据相似三角形的判定定理(两边对应成比例且夹角相等的两个三角形相似),可得$△ ABD∼△ ACB$。
所以$\frac{AB}{AC}=\frac{BD}{CB}$,因为$AB = AC$,所以$BD = BC$。
设$∠ A=α$,因为$△ ABD∼△ ACB$,所以$∠ ABD=∠ C$。
又因为$AB = AC$,所以$∠ ABC=∠ C$。
根据三角形内角和定理$∠ A+∠ ABC+∠ C = 180^{\circ}$,即$α + 2∠ C=180^{\circ}$。
由$△ ABD∼△ ACB$,$\frac{AD}{AB}=\frac{AB}{AC}$($AB = AC$),$\cos A=\frac{AD^{2}+AC^{2}-CD^{2}}{2AD· AC}$,由$AD^{2}=AC· CD$,$AC = 1$,$AD=\frac{\sqrt{5}-1}{2}$,$CD=\frac{3 - \sqrt{5}}{2}$。
$\cos A=\frac{(\frac{\sqrt{5}-1}{2})^{2}+1^{2}-(\frac{3 - \sqrt{5}}{2})^{2}}{2×\frac{\sqrt{5}-1}{2}×1}$
先计算分子:$(\frac{\sqrt{5}-1}{2})^{2}+1-(\frac{3 - \sqrt{5}}{2})^{2}=\frac{5 - 2\sqrt{5}+1}{4}+1-\frac{9 - 6\sqrt{5}+5}{4}=\frac{6 - 2\sqrt{5}+4-(14 - 6\sqrt{5})}{4}=\frac{10 - 2\sqrt{5}-14 + 6\sqrt{5}}{4}=\frac{4\sqrt{5}-4}{4}=\sqrt{5}-1$。
分母$=\sqrt{5}-1$,所以$\cos A=\frac{\sqrt{5}-1}{2}$,则$∠ A = 36^{\circ}$。
因为$∠ A+∠ ABC+∠ C = 180^{\circ}$,$∠ ABC=∠ C$,所以$∠ C=∠ ABD = 72^{\circ}$。
综上,(1)证明过程如上述;(2)$∠ ABD = 36^{\circ}$。
16. 如图,抛物线$y = x^{2}-x - 1$与$y$轴交于点$C$,以原点$O$为圆心,$OC$长为半径作$\odot O$,交$x$轴于$A$,$B$两点,交$y$轴于另一点$D$.设点$P$为抛物线$y = x^{2}-x - 1$上的一点,作$PM⊥ x$轴于点$M$,求使$△ PMB∽△ ADB$时点$P$的坐标.
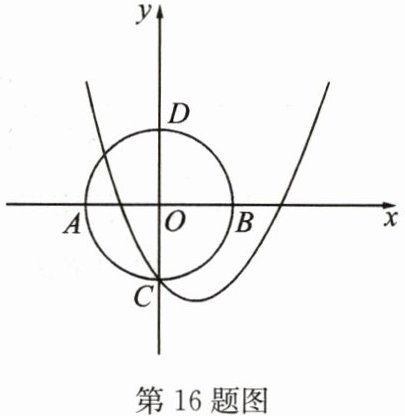

答案:
16. 设点$P$的横坐标$x_{P}=a$,则点$P$的纵坐标$y_{P}=a^{2}-a - 1$。则$PM = |a^{2}-a - 1|$,$BM = |a - 1|$。因为$△ ADB$为等腰直角三角形,所以欲使$△ PMB∽△ ADB$,只要使$PM = BM$。即$|a^{2}-a - 1| = |a - 1|$。不难得$a_{1}=0$,$a_{2}=2$,$a_{3}=\sqrt{2}$,$a_{4}=-\sqrt{2}$。$\therefore$点$P$坐标分别为$P_{1}(0,-1)$,$P_{2}(2,1)$,$P_{3}(\sqrt{2},1-\sqrt{2})$,$P_{4}(-\sqrt{2},1+\sqrt{2})$
查看更多完整答案,请扫码查看


