《2026年长江作业本同步练习册九年级数学下册人教版》

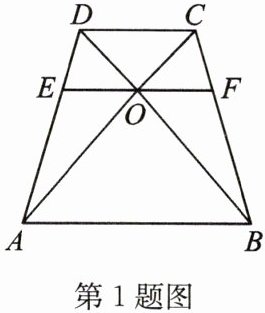
1. 如图，在梯形 $ABCD$ 中，$AB // DC$，对角线 $AC$，$BD$ 交于点 $O$，过 $O$ 作 $EF // AB$ 分别交 $AD$，$BC$ 于点 $E$，$F$。求证：$\frac{1}{AB} + \frac{1}{CD} = \frac{1}{EO}$。

答案： 1. $\because EF// AB,AB// DC,\therefore EF// DC,\therefore △ AOE∽ △ ACD,△ DOE∽ △ DBA,\therefore \frac{EO}{CD}=\frac{AE}{AD},\frac{EO}{AB}=\frac{DE}{AD},\therefore \frac{EO}{CD}+\frac{EO}{AB}=\frac{AE}{AD}+\frac{DE}{AD}=1,\therefore \frac{1}{AB}+\frac{1}{CD}=\frac{1}{EO}$

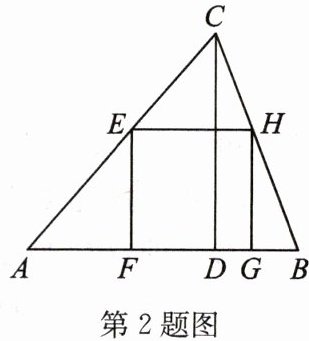
2. 如图，在 $△ ABC$ 中，已知 $CD$ 为边 $AB$ 上的高，正方形 $EFGH$ 的四个顶点分别在 $△ ABC$ 上。求证：$\frac{1}{AB} + \frac{1}{CD} = \frac{1}{EF}$。

答案： 2. $\because EF// CD,EH// AB,\therefore ∠ AFE=∠ ADC,∠ CEH=∠ A.\because ∠ A=∠ A,∠ ECH=∠ BCA,\therefore △ AFE∽ △ ADC,△ CEH∽ △ CAB.\therefore \frac{AE}{AC}=\frac{EF}{CD},\frac{CE}{AC}=\frac{EH}{AB}.\because EF=EH,\therefore \frac{EF}{AB}+\frac{EF}{CD}=\frac{EH}{AB}+\frac{EF}{CD}=\frac{CE}{AC}+\frac{AE}{AC}=1\therefore \frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$

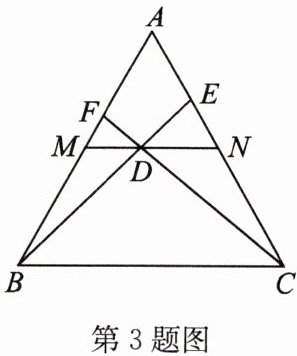
3. 如图，在等边 $△ ABC$ 中，$M$，$N$ 分别是边 $AB$，$AC$ 的中点，$D$ 为 $MN$ 上任意一点，$BD$，$CD$ 的延长线分别交 $AC$，$AB$ 于点 $E$，$F$。求证：$\frac{1}{CE} + \frac{1}{BF} = \frac{3}{AB}$。

答案： 3. 作$DP// AB,DQ// AC$,则四边形$MDPB$和四边形$NDQC$均为平行四边形且$△ DPQ$是等边三角形.$\therefore BP+CQ=MN,DP=DQ=PQ.\because M,N$分别是边$AB,AC$的中点,$\therefore MN=\frac{1}{2}BC=PQ.\because DP// AB,DQ// AC,\therefore △ CDP∽ △ CFB,△ BDQ∽ △ BEC,\therefore \frac{DP}{BF}=\frac{CP}{BC},\frac{DQ}{CE}=\frac{BQ}{BC},\therefore \frac{DP}{BF}+\frac{DQ}{CE}=\frac{CP}{BC}+\frac{BQ}{BC}=\frac{BC+PQ}{BC}=\frac{3}{2}.\because DP=DQ=PQ=\frac{1}{2}BC=\frac{1}{2}AB,\therefore \frac{1}{2}AB(\frac{1}{CE}+\frac{1}{BF})=\frac{3}{2},\therefore \frac{1}{CE}+\frac{1}{BF}=\frac{3}{AB}$