《2025年全科王同步课时练习七年级数学上册人教版》

8. (2024·天津和平区期末)若单项式$\frac{1}{3}a^{m + 1}b^{3}$与-2a^3bⁿ的和仍是单项式,则方程$\frac{x - 7}{n}-\frac{1 + x}{m}= 1$的解为 (A)
A.x = -23
B.x = 23
C.x = -29
D.x = 29

答案： A[提示:因为单项式$\frac{1}{3}a^{m+1}b^{3}$与$-2a^{3}b^{n}$的和仍是单项式,所以m+1=3,n=3,解得m=2.所以$\frac{x-7}{3}-\frac{1+x}{2}=1$.去分母,得2(x-7)-3(1+x)=6,去括号,得2x-14-3-3x=6,移项,得2x-3x=6+14+3,合并同类项,得-x=23,系数化为1,得x=-23.]

9. (2024·四川巴中期末)对于两个不相等的有理数a,b,我们规定符号max{a,b}表示a,b两数中较大的数,例如max{2,4}= 4,max{-2,-4}= -2.按照这个规定,那么方程max{x,5x}= 2x + 6的解为 (C)
A.x = 2
B.x = 3或x = -6
C.x = 2或x = -6
D.x = 3

答案： C[提示:当x＞5x时,得x=2x+6,解得x=-6.因为5×(-6)=-30,且-6＞-30,所以x=-6是该方程的解.当x＜5x时,得5x=2x+6,解得x=2.因为5×2=10,且2＜10,所以x=2是该方程的解.]

10. 如图,若开始输入的x的值为正整数,最后输出的结果为114,则满足条件的x的值为23.

答案： 23[提示:若第一个数输出的结果为114,则5x-1=114,解得x=23.若第二个数输出的结果为114,则5(5x-1)-1=114,解得x=4.8(不合题意,舍去).]

11. 小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(3)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?

答案： 解:
(1)设x秒后两人相遇,则小彬跑了4x米,小明跑了6x米,由题意,得6x+4x=100,解得x=10.答:10秒后两人相遇.
(2)设y秒后小明能追上小彬,根据题意,得小明跑了6y米,小彬跑了4y米,由题意,得6y-4y=10,解得y=5.答:两人同时同向起跑,5秒后小明能追上小彬.
(3)设a秒后他们再次相遇,由题意,得6a-4a=400,解得a=200.200秒=$\frac{10}{3}$分钟.答:$\frac{10}{3}$分钟后他们再次相遇.

12. (2023·四川凉山州期末)历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示.例如f(x)= x^2 + 3x - 5,把“x = 某数”时多项式的值用f(某数)来表示.例如当x = -1时,多项式x^2 + 3x - 5的值记为f(-1)= (-1)^2 + 3×(-1) - 5 = -7.
(1)已知g(x)= -2x^2 - 3x + 1,分别求出g(-1)和g(-2)的值;
(2)已知h(x)= ax^3 + 2x^2 - x - 14,$h(\frac{1}{2})= a$,求a的值.

答案： 解:
(1)由题意,得g(-1)=-2(-1)$^{2}$-3×(-1)+1=2,g(-2)=-2(-2)$^{2}$-3×(-2)+1=-1.
(2)由题意,得$\frac{1}{8}a+\frac{1}{2}-\frac{1}{2}-14=a$,解得a=-16.

13. 某超市元旦期间搞促销活动,活动方案如下表:

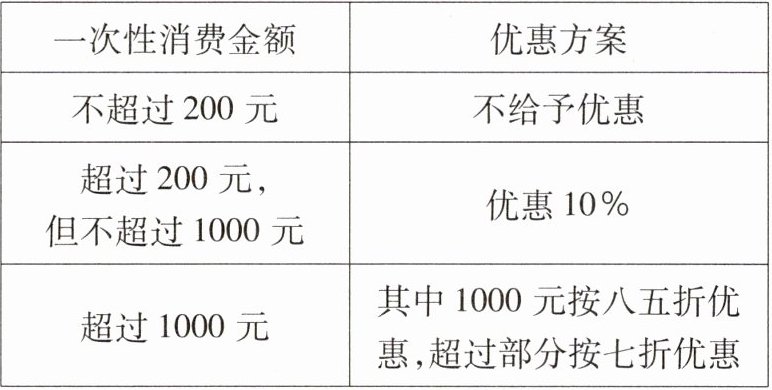
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的商品如果不打折,一共应支付多少钱?
(2)在此次活动中,小颖节省了多少钱?

答案： 解:
(1)①因为134＜200×90%=180,所以第一次购物小颖不享受优惠;②因为第二次支付了913元,且913＞1000×85%=850,所以其中1000元按八五折优惠,超过1000元的部分按七折优惠.设小颖第二次购买了价值x元的商品,根据题意,得85%×1000+(x-1000)×70%=913,解得x=1090,1090+134=1224(元).答:小颖两次购买的商品如果不打折,一共应支付1224元钱.
(2)1090-913=177(元).答:在此次活动中,小颖节省了177元钱.