第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2023·山东临沂中考)计算$(-7)-(-5)$的结果是(
A.-12
B.12
C.-2
D.2
C
)A.-12
B.12
C.-2
D.2
答案:
C[提示:原式=(-7)+5=-2.]
2. (2023·山东滨州中考)计算$2-|-3|$的结果为
-1
。
答案:
-1[提示:原式=2-3=-(3-2)=-1.]
3. (2023·山东泰安中考)$-\frac{2}{3}$的倒数是(
A.$-\frac{3}{2}$
B.$\frac{3}{2}$
C.$\frac{2}{3}$
D.$-\frac{2}{3}$
A
)A.$-\frac{3}{2}$
B.$\frac{3}{2}$
C.$\frac{2}{3}$
D.$-\frac{2}{3}$
答案:
A
4. (2023·天津中考)计算$(-\frac{1}{2})×(-2)$的结果等于(
A.$-\frac{5}{2}$
B.-1
C.$\frac{1}{4}$
D.1
D
)A.$-\frac{5}{2}$
B.-1
C.$\frac{1}{4}$
D.1
答案:
D
5. (2023·辽宁营口中考)有下列四个算式:①$(-5)+(+3)= -8$;②$-(-2)^{3}= 6$;③$(+\frac{5}{6})+(-\frac{1}{6})= \frac{2}{3}$;④$-3÷(-\frac{1}{3})= 9$。其中,正确的有(
A.0 个
B.1 个
C.2 个
D.3 个
C
)A.0 个
B.1 个
C.2 个
D.3 个
答案:
C[提示:①(-5)+(+3)=-2,原来的计算错误;②-(-2)³=8,原来的计算错误;③(+5/6)+(-1/6)=2/3,原来的计算正确;④-3÷(-1/3)=9,原来的计算正确.正确的有2个.]
6. (2023·湖北随州中考)计算:$(-2)^{2}+(-2)×2= $
0
。
答案:
0[提示:(-2)²+(-2)×2=4+(-4)=0.]
7. (2023·四川资阳中考)计算机的二进制数据是用 0 和 1 两个数码来表示的数,进位规则是“逢二进一”,二进制数和十进制数可以互换,例如,二进制数“01011011”换成十进制数表示的数为$0×2^{7}+1×2^{6}+0×2^{5}+1×2^{4}+1×2^{3}+0×2^{2}+1×2^{1}+1×2^{0}= 91$。依此算法,二进制数“01001001”换成十进制数表示的数为
73
。
答案:
73[提示:由题意,得01001001=0×2⁷+1×2⁶+0×2⁵+0×2⁴+1×2³+0×2²+0×2¹+1×2⁰=73.]
8. (2023·广西中考)计算$(-1)×(-4)+2^{2}÷(7-5)$。
答案:
解:原式=(-1)×(-4)+4÷2=4+2=6.
9. (2024·江苏连云港中考)2024 年 5 月,全国最大的海上光伏项目获批落地连云港,批准用海面积约 28000 亩,总投资约 90 亿元。其中数据“28000”用科学记数法可以表示为(
A.$28×10^{3}$
B.$2.8×10^{4}$
C.$2.8×10^{3}$
D.$0.28×10^{5}$
B
)A.$28×10^{3}$
B.$2.8×10^{4}$
C.$2.8×10^{3}$
D.$0.28×10^{5}$
答案:
B
10. (2024·上海中考)科学家研发了一种新的蓝光唱片,一张蓝光唱片的容量约为$2×10^{5}GB$,一张普通唱片的容量约为 25 GB,则蓝光唱片的容量是普通唱片的
8×10³
倍。(用科学记数法表示)
答案:
8×10³[提示:2×10⁵=200000,则200000÷25=8000=8×10³,即蓝光唱片的容量是普通唱片的8×10³倍.]
11. (2023·辽宁丹东东港市期中)有理数 a,b,c 在数轴上的位置如图,则下列各式:①$bc>0$;②$c>b$;③$c-a<0$;④$|a-b|= b-a$。正确的有(
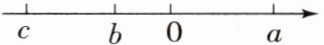
A.1 个
B.2 个
C.3 个
D.4 个
B
)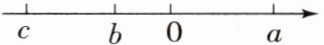
A.1 个
B.2 个
C.3 个
D.4 个
答案:
B[提示:由数轴知b,c同号,所以bc>0,①正确.c<b,②不正确.因为c<0,a>0,所以c-a<0,③正确.因为a>b,所以a-b>0,所以|a-b|=a-b,④不正确.]
12. 用“*”定义新运算,对于任意有理数 a,b,都有$a*b= b^{3}-1$,则$\frac{1}{2}*[3*(-1)]$的值为(
A.-1
B.-9
C.$-\frac{1}{2}$
D.0
-9
)A.-1
B.-9
C.$-\frac{1}{2}$
D.0
答案:
B[提示:因为a*b=b³-1,所以1/2*[3*(-1)]=1/2*[(-1)³-1]=1/2*[(-1)-1]=1/2*(-2)=(-2)³-1=(-8)-1=-9.]
13. (2024·辽宁营口期中)小涵同学在做有理数的计算时发现:$\frac{1}{1×3}= \frac{1}{2}×(1-\frac{1}{3})$;$\frac{1}{3×5}= \frac{1}{2}×(\frac{1}{3}-\frac{1}{5})$;$\frac{1}{5×7}= \frac{1}{2}×(\frac{1}{5}-\frac{1}{7})$;$\frac{1}{7×9}= \frac{1}{2}×(\frac{1}{7}-\frac{1}{9})$。请根据小涵发现的规律,计算$\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+\frac{1}{63}+... +\frac{1}{9999}$的值为(
A.$\frac{50}{101}$
B.$\frac{100}{101}$
C.$\frac{200}{101}$
D.$\frac{5000}{5001}$
A
)A.$\frac{50}{101}$
B.$\frac{100}{101}$
C.$\frac{200}{101}$
D.$\frac{5000}{5001}$
答案:
A[提示:1/3+1/15+1/35+1/63+…+1/9999=1/(1×3)+1/(3×5)+1/(5×7)+1/(7×9)+…+1/(99×101)=1/2×(1-1/3)+1/2×(1/3-1/5)+1/2×(1/5-1/7)+1/2×(1/7-1/9)+…+1/2×(1/99-1/101)=1/2×(1-1/3+1/3-1/5+1/5-1/7+1/7-1/9+…+1/99-1/101)=1/2×(1-1/101)=1/2×100/101=50/101.]
查看更多完整答案,请扫码查看


