第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. 下列变形不正确的是(
A.$5×(-6) = (-6)×5$
B.$(\dfrac{1}{4}-\dfrac{1}{2})×(-12) = (-12)×(\dfrac{1}{4}-\dfrac{1}{2})$
C.$(-\dfrac{1}{6}+\dfrac{1}{3})×(-4) = (-4)×(-\dfrac{1}{6})+\dfrac{1}{3}×4$
D.$(-25)×(-16)×(-4) = [(-25)×(-4)]×(-16)$
C
)A.$5×(-6) = (-6)×5$
B.$(\dfrac{1}{4}-\dfrac{1}{2})×(-12) = (-12)×(\dfrac{1}{4}-\dfrac{1}{2})$
C.$(-\dfrac{1}{6}+\dfrac{1}{3})×(-4) = (-4)×(-\dfrac{1}{6})+\dfrac{1}{3}×4$
D.$(-25)×(-16)×(-4) = [(-25)×(-4)]×(-16)$
答案:
C
11. 按如图所示的运算程序,能使输出结果为$3的x$,$y$的值分别是(
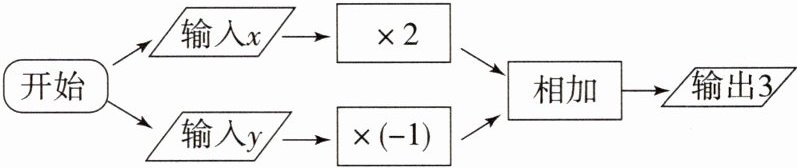
A.$5$,$-2$
B.$3$,$-3$
C.$-3$,$-9$
D.$-4$,$2$
C
)
A.$5$,$-2$
B.$3$,$-3$
C.$-3$,$-9$
D.$-4$,$2$
答案:
C
12. (2024·天津河东区期末)四个各不相等的整数a,b,c,d满足abcd = 9,则a + b + c + d的值为(
A.$0$
B.$4$
C.$10$
D.无法确定
A
)A.$0$
B.$4$
C.$10$
D.无法确定
答案:
A
13. 五个有理数的积为负数,则这五个数中负因数有
1或3或5
个。
答案:
1或3或5
14. (易错题)用简便方法计算.
(1)$(-9)×31\dfrac{8}{29}-(-8)×(-31\dfrac{8}{29})-(-16)×31\dfrac{8}{29}$;
(2)$3.95×6 - 1.95×6 + (\dfrac{7}{9}-\dfrac{5}{6}-\dfrac{5}{18})×(-18)$。
(1)$(-9)×31\dfrac{8}{29}-(-8)×(-31\dfrac{8}{29})-(-16)×31\dfrac{8}{29}$;
(2)$3.95×6 - 1.95×6 + (\dfrac{7}{9}-\dfrac{5}{6}-\dfrac{5}{18})×(-18)$。
答案:
(1) 原式$=(-9 - 8 + 16) × 31\dfrac{8}{29}$
$=(-1) × 31\dfrac{8}{29}$
$=-31\dfrac{8}{29}$
(2) 原式$=(3.95 - 1.95) × 6 + \left(\dfrac{7}{9} × (-18) - \dfrac{5}{6} × (-18) - \dfrac{5}{18} × (-18)\right)$
$=2 × 6 + (-14 + 15 + 5)$
$=12 + 6$
$=18$
(1) 原式$=(-9 - 8 + 16) × 31\dfrac{8}{29}$
$=(-1) × 31\dfrac{8}{29}$
$=-31\dfrac{8}{29}$
(2) 原式$=(3.95 - 1.95) × 6 + \left(\dfrac{7}{9} × (-18) - \dfrac{5}{6} × (-18) - \dfrac{5}{18} × (-18)\right)$
$=2 × 6 + (-14 + 15 + 5)$
$=12 + 6$
$=18$
15. 一儿童服装店老板以$32元的价格购进30$件连衣裙,针对不同的顾客,$30$件连衣裙的售价不完全相同,若以$47$元为标准价,将超过的钱数记为正,不足的钱数记为负,则记录结果如下表:

(1)该服装店售完这$30$件连衣裙的总销售额是多少?
(2)该服装店售完这$30$件连衣裙赚了多少钱?

(1)该服装店售完这$30$件连衣裙的总销售额是多少?
(2)该服装店售完这$30$件连衣裙赚了多少钱?
答案:
(2)1432-32×30=1432-960=472(元).答:该服装店老板售完这30件连衣裙赚了472元.
(2)1432-32×30=1432-960=472(元).答:该服装店老板售完这30件连衣裙赚了472元.
16. 观察下列各式:
$-1×\dfrac{1}{2} = -1+\dfrac{1}{2}$;
$-\dfrac{1}{2}×\dfrac{1}{3} = -\dfrac{1}{2}+\dfrac{1}{3}$;
$-\dfrac{1}{3}×\dfrac{1}{4} = -\dfrac{1}{3}+\dfrac{1}{4}$;
…
(1)分别写出第$4个等式和第5$个等式;
(2)用规律计算:$(-1×\dfrac{1}{2})+(-\dfrac{1}{2}×\dfrac{1}{3})+(-\dfrac{1}{3}×\dfrac{1}{4})+…+(-\dfrac{1}{2022}×\dfrac{1}{2023})+(-\dfrac{1}{2023}×\dfrac{1}{2024})$。
$-1×\dfrac{1}{2} = -1+\dfrac{1}{2}$;
$-\dfrac{1}{2}×\dfrac{1}{3} = -\dfrac{1}{2}+\dfrac{1}{3}$;
$-\dfrac{1}{3}×\dfrac{1}{4} = -\dfrac{1}{3}+\dfrac{1}{4}$;
…
(1)分别写出第$4个等式和第5$个等式;
(2)用规律计算:$(-1×\dfrac{1}{2})+(-\dfrac{1}{2}×\dfrac{1}{3})+(-\dfrac{1}{3}×\dfrac{1}{4})+…+(-\dfrac{1}{2022}×\dfrac{1}{2023})+(-\dfrac{1}{2023}×\dfrac{1}{2024})$。
答案:
16.解:
(1)观察各个式子可以发现:这3个式子中等号左边的规律:“×”前面的负数中分子都是1,第1个式子的分母是1,第2个式子的分母是2,第3个式子的分母是3,所以可推出第4个式子的分母是4,第5个式子的分母是5,第n个式子的分母是n;“×”后面的分数中,分子都是1,第1个式子的分母是2,第2个式子的分母是3,第3个式子的分母是4,所以可推出第4个式子的分母是5,第5个式子的分母是6,第n个式子的分母是n+1;这3个式子中等号右边的规律是把等号左边式子中的“×”改为“+”.所以第4个等式为:$-\frac{1}{4}×\frac{1}{5}=-\frac{1}{4}+\frac{1}{5}$,第5个式子为:$-\frac{1}{5}×\frac{1}{6}=-\frac{1}{5}+\frac{1}{6}$.
(2)由
(1)中的规律得$-\frac{1}{n}×\frac{1}{n+1}=-\frac{1}{n}+\frac{1}{n+1}$,所以$\left(-1×\frac{1}{2}\right)+\left(-\frac{1}{2}×\frac{1}{3}\right)+\left(-\frac{1}{3}×\frac{1}{4}\right)+\cdots+\left(-\frac{1}{2022}×\frac{1}{2023}\right)+\left(-\frac{1}{2023}×\frac{1}{2024}\right)=-1+\frac{1}{2}-\frac{1}{2}+\frac{1}{3}-\frac{1}{3}+\frac{1}{4}+\cdots-\frac{1}{2022}+\frac{1}{2023}-\frac{1}{2023}+\frac{1}{2024}=-1+\frac{1}{2024}=-\frac{2023}{2024}$.
(1)观察各个式子可以发现:这3个式子中等号左边的规律:“×”前面的负数中分子都是1,第1个式子的分母是1,第2个式子的分母是2,第3个式子的分母是3,所以可推出第4个式子的分母是4,第5个式子的分母是5,第n个式子的分母是n;“×”后面的分数中,分子都是1,第1个式子的分母是2,第2个式子的分母是3,第3个式子的分母是4,所以可推出第4个式子的分母是5,第5个式子的分母是6,第n个式子的分母是n+1;这3个式子中等号右边的规律是把等号左边式子中的“×”改为“+”.所以第4个等式为:$-\frac{1}{4}×\frac{1}{5}=-\frac{1}{4}+\frac{1}{5}$,第5个式子为:$-\frac{1}{5}×\frac{1}{6}=-\frac{1}{5}+\frac{1}{6}$.
(2)由
(1)中的规律得$-\frac{1}{n}×\frac{1}{n+1}=-\frac{1}{n}+\frac{1}{n+1}$,所以$\left(-1×\frac{1}{2}\right)+\left(-\frac{1}{2}×\frac{1}{3}\right)+\left(-\frac{1}{3}×\frac{1}{4}\right)+\cdots+\left(-\frac{1}{2022}×\frac{1}{2023}\right)+\left(-\frac{1}{2023}×\frac{1}{2024}\right)=-1+\frac{1}{2}-\frac{1}{2}+\frac{1}{3}-\frac{1}{3}+\frac{1}{4}+\cdots-\frac{1}{2022}+\frac{1}{2023}-\frac{1}{2023}+\frac{1}{2024}=-1+\frac{1}{2024}=-\frac{2023}{2024}$.
查看更多完整答案,请扫码查看


