《2025年全科王同步课时练习七年级数学上册人教版》

8. 阅读下面材料并解决有关问题：
我们知道：$\vert x\vert = \begin{cases} x(x ＞ 0), \\ 0(x = 0), \\ -x(x ＜ 0). \end{cases} $现在我们可以用这一结论来化简含有绝对值的式子,如化简$\vert x + 1\vert + \vert x - 2\vert$时,可令$x + 1 = 0和x - 2 = 0$,分别求得$x = -1$,$x = 2$(称-1,2分别为$\vert x + 1\vert与\vert x - 2\vert$的零点值). 零点值$x = -1和x = 2$可将全体数分成不重复且不遗漏的如下三种情况：
①$x ＜ -1$；②$-1 \leq x ＜ 2$；③$x \geq 2$.
从而化简$\vert x + 1\vert + \vert x - 2\vert$可分以下三种情况：
①当$x ＜ -1$时,原式$= -(x + 1) - (x - 2) = -x - 1 - x + 2 = -2x + 1$；
②当$-1 \leq x ＜ 2$时,原式$= x + 1 - (x - 2) = x + 1 - x + 2 = 3$；
③当$x \geq 2$时,原式$= x + 1 + x - 2 = 2x - 1$.
综上,原式$= \begin{cases} -2x + 1(x ＜ -1), \\ 3(-1 \leq x ＜ 2), \\ 2x - 1(x \geq 2). \end{cases} $
通过阅读以上材料,请你解决以下问题：
(1) 化简$\vert x + 2\vert + \vert x - 4\vert$；
(2) 求$\vert x - 1\vert - 4\vert x + 1\vert$的最大值.

答案： 8.解:
(1)由x+2=0,得x=-2;由x-4=0,得x=4.当x＜-2时,|x+2|+|x-4|=-x-2+4-x=-2x+2;当-2≤x＜4时,|x+2|+|x-4|=x+2+4-x=6;当x≥4时,|x+2|+|x-4|=x+2+x-4=2x-2.综上,原式=$\begin{cases}-2x+2(x＜-2),\\6(-2\leqslant x＜4),\\2x-2(x\geqslant4).\end{cases}$
(2)由x-1=0,得x=1;由x+1=0,得x=-1.当x＜-1时,原式=3x+5,3x+5＜2;当-1≤x≤1时,原式=-5x-3,-8≤-5x-3≤2;当x＞1时,原式=-3x-5,-3x-5＜-8.则|x-1|-4|x+1|的最大值为2.

9. 已知$a ＜ -1$,$-1 \leq c \leq 0$,$a ＜ b ＜ c$,求$\vert a + b + c\vert - \vert b - c\vert - \vert a - c - 1\vert$的最大值和最小值.

答案： 9.解:因为a＜-1,-1≤c≤0,a＜b＜c,所以a+b+c＜0,b-c＜0,a-c-1＜0,所以|a+b+c|-|b-c|-|a-c-1|=-(a+b+c)-(c-b)-(c-a+1)=-a-b-c-c+b-c+a-1=-3c-1.因为-1≤c≤0,所以-3≤3c≤0,所以-1≤-3c-1≤2.所以最小值为-1,最大值为2.

10. (2024·江苏南通海安市期中)阅读下列材料,并回答问题. 我们知道$\vert a\vert$的几何意义是指数轴上表示数a的点与原点的距离,那么$\vert a - b\vert$的几何意义又是什么呢？我们不妨考虑一下,取特殊值时的情况. 比如考虑$\vert 5 - (-6)\vert$的几何意义,在数轴上分别标出表示-6和5的点,(如图),两点间的距离是11,而$\vert 5 - (-6)\vert = 11$,因此不难看出$\vert 5 - (-6)\vert$就是数轴上表示-6和5两点间的距离,$\vert a - b\vert$的几何意义是数轴上a,b两数对应点之间的距离.

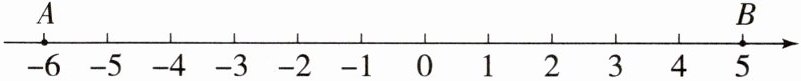
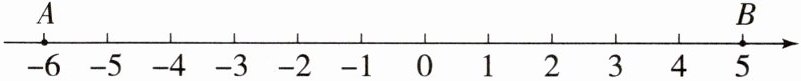
(1) 当$\left\vert x - \frac{2}{3}\right\vert = 2$时,求出x的值.
(2) 设$Q = \vert x + 6\vert - \vert x - 5\vert$,则Q是否存在最大值,若没有,请说明理由；若有,请求出最大值.
(3) 设$Q = \vert x + 2023\vert + \vert 2024 + x\vert + 2\vert 2026 - x\vert$,当Q的值最小时,求整数x所有可能的值的和.

答案： 10.解:
(1)当$|x-\frac{2}{3}|=2$时,$x-\frac{2}{3}=2$或-2,解得$x=\frac{8}{3}$或$-\frac{4}{3}$.
(2)Q=|x+6|-|x-5|存在最大值,为11.理由:分三种情况:当x≤-6时,Q=|x+6|-|x-5|=-x-6+x-5=-11;当-6＜x≤5时,Q=|x+6|-|x-5|=x+6+x-5=2x+1,则-11＜2x+1≤11;当x＞5时,Q=|x+6|-|x-5|=x+6-(x-5)=11.所以Q的最大值为11.
(3)Q=|x+2023|+|2024+x|+2|2026-x|,当x＜-2024时,Q=|x+2023|+|2024+x|+2|2026-x|=-x-2023-2024-x+2(2026-x)=-4x+5＞8091.当-2024≤x＜-2023时,Q=|x+2023|+|2024+x|+2|2026-x|=-x-2023+2024+x+2(2026-x)=4053-2x,而8099＜4053-2x≤8101.当-2023≤x≤2026时,Q=|x+2023|+|2024+x|+2|2026-x|=x+2023+2024+x+2(2026-x)=8099.当x＞2026时,Q=|x+2023|+|2024+x|+2|2026-x|=x+2023+2024+x+2(x-2026)=4x-5＞8099.所以Q=|x+2023|+|2024+x|+2|2026-x|的最小值为8099,此时-2023≤x≤2026.所以整数x所有可能的值的和为-2023-2022-2021-2020-…-2-1+0+1+2+…+2023+2024+2025+2026=0+2024+2025+2026=6075.