《2025年全科王同步课时练习七年级数学上册人教版》

12. (易错题)多项式$x^{|m|}-(m-4)x+7是关于x$的四次三项式,则$m$的值是(-4)
A.-2
B.4
C.-4
D.4或-4

答案： 12.C[提示:因为多项式$x^{|m|}-(m-4)x+7$是关于x的四次三项式,所以$\left\{\begin{array}{l} |m|=4,\\ m-4≠0,\end{array}\right. $解得$m=-4.]$

13. (2024·广东广州越秀区期中)随着计算机技术的迅猛发展,电脑价格不断降低.某品牌电脑按原售价降低$m$元后,又降低$10\%$,现售价为$n$元,那么该电脑的原售价为(B)
A.$(\frac {9}{10}n+m)$元
B.$(\frac {10}{9}n+m)$元
C.$(10m+n)$元
D.$(10n+m)$元

答案： 13.B

14. 单项式$-2a^{2}b的系数是m$,多项式$-xy^{3}+2x^{2}y^{3}-3的次数是n$,则$m+n$的值为3.

答案： 14.3[提示:因为单项式$-2a^{2}b$的系数是m,所以$m=-2$.因为多项式$-xy^{3}+2x^{2}y^{3}-3$的次数是n,所以$n=5$,则$m+n=-2+5=3.]$

15. 已知多项式$-3x^{5}y^{m-1}-2x^{3}+7+my^{4}-y^{2}是关于x,y$的八次五项式.求该多项式的四次项.

答案： 15.解:因为多项式$-3x^{5}y^{m-1}-2x^{3}+7+my^{4}-y^{2}$是关于x,y的八次五项式,所以$5+m-1=8$,即$m=4$,故该多项式为$-3x^{5}y^{3}-2x^{3}+7+4y^{4}-y^{2}$,所以该多项式的四次项是$4y^{4}.$

16. 已知关于$x的整式(|k|-3)x^{3}+(k-3)x^{2}-k$.
(1) 若此整式是单项式,求$k$的值;
(2) 若此整式是二次多项式,求$k$的值.

答案： 16.解:
(1)因为关于x的整式是单项式,所以$|k|-3=0$且$k-3=0$,解得$k=3$,所以k的值是3.
(2)因为关于x的整式是二次多项式,所以$|k|-3=0$且$k-3≠0$,解得$k=-3$,所以k的值是-3.

17. (2024·广东湛江徐闻县期末)某村种植了土豆、玉米、水稻三种农作物,土豆种植面积是$a$亩,水稻种植面积是土豆种植面积的3倍,玉米种植面积比土豆种植面积的2倍少2亩.
(1) 求水稻、玉米的种植面积;(用含$a$的式子表示)
(2) 判断这两个式子是单项式还是整式,它们的次数是多少?

答案： 17.解:
(1)因为土豆种植面积是a亩,水稻种植面积是土豆种植面积的3倍,所以水稻种植面积为3a亩.因为玉米种植面积比土豆种植面积的2倍少2亩,所以玉米种植面积为$(2a-2)$亩.
(2)3a是单项式,次数是1;$2a-2$是多项式,次数是1.

18. 某餐厅中,一张桌子可坐6人,如果把多张桌子摆在一起,可以有以下两种摆放方式(如图所示):

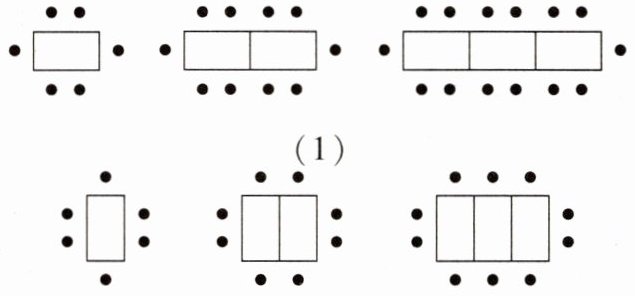
(1) 当有$n$张桌子时,两种摆放方式各能坐多少人?
(2) 一天中午餐厅要接待98位顾客共同就餐(即桌子要摆在一起),但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌？为什么?

答案： 18.解:
(1)第一种摆放方式能坐$(4n+2)$人,第二种摆放方式能坐$(2n+4)$人.
(2)打算用第一种摆放方式来摆放餐桌.因为当$n=25$时,$4×25+2=102,102＞98$,当$n=25$时,$2×25+4=54,54＜98$,所以选用第一种摆放方式.