《2025年全科王同步课时练习七年级数学上册人教版》

11. (2023·福建厦门湖里区期中)有一种记分方法：以$80$分为标准,$88分记为+8$分. 某同学得分为$75$分,则应记为(D)
A.$+75$分
B.$-75$分
C.$+5$分
D.$-5$分

答案： D

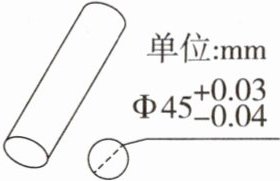
12. (2024·山东莱西市期中)如图是加工某零件的尺寸要求,现有下列直径尺寸的产品(单位：$mm$),其中不合格的是(A)


A.$\Phi45.04$
B.$\Phi44.96$
C.$\Phi44.98$
D.$\Phi45.02$

答案： A[提示:因为45+0.03=45.03,45-0.04=44.96,所以零件的直径尺寸的合格范围是:44.96≤零件的直径尺寸≤45.03.因为45.04不在该范围之内,所以不合格的是A.]

13. 若规定体育成绩$80$分为标准,超过记为“正”,不足记为“负”,老师将三名同学的成绩记为：$+18,-14,0$,则这三名同学的实际成绩中最高分数是98分.

答案： 98分[提示:由题意,得80+18=98(分),80-14=66(分),80+0=80(分).因为98＞80＞66,所以这三名同学的实际成绩中最高分数是98分.]

14. 小瑞规定早上七点起床作为标准时间,早于七点起床记为正,迟于七点起床记为负,如果早上$6:50$起床记为“$+10$”,那么周末的时候,小瑞早上起床时间记为“$-35$”,则小瑞早上起床时间是7:35.

答案： 7:35[提示:因为早于七点起床记为正,迟于七点起床记为负,早上6:50起床记为"+10",所以记为"-35"的起床时间是7:35.]

15. 下面各数：$2,-3,+1,\frac{1}{3},-1.5,0,0.2,3\frac{1}{4},-4\frac{3}{5}$. 哪些是正数？哪些是负数？

答案： 解:正数:2,+1,$\frac{1}{3}$,0.2,$3\frac{1}{4}$.负数:-3,-1.5,$-4\frac{3}{5}$.

16. 教室天花板距离地面$2.8m$,桌面高出地面$0.6m$.
(1)如果把地面记作$0m$,地面以上记为正,那么天花板和桌面分别记作什么？
(2)如果把天花板记作$0m$,天花板以下记为负,那么桌面和地面分别记作什么？

答案： 解:
(1)天花板记作+2.8m,桌面记作+0.6m.
(2)桌面记作-2.2m,地面记作-2.8m.

17. 某中学对七年级男生进行引体向上的测试,以能做$7$个为标准,超过的个数用正数表示,不足的个数用负数表示,其中$8$人的成绩如下：$0,1,-3,-2,3,0,-1,2$.
(1)这$8$人中有几人达标？
(2)达标率是多少？
(3)他们共做了多少个引体向上？

答案： 解:
(1)因为超过的个数用正数表示,不足的个数用负数表示,其中8人的成绩如下:0,1,-3,-2,3,0,-1,2,所以这8人中有5人达标.
(2)达标率是$\frac{5}{8}$×100%=62.5%.
(3)因为7+0=7,7+1=8,7-3=4,7-2=5,7+3=10,7+0=7,7-1=6,7+2=9,所以他们共做引体向上7+8+4+5+10+7+6+9=56(个).

18. 观察下面一列数：$-1,+2,-3,+4,-5,+6,-7,+8,-9,…$.
(1)请写出这一列数中的第$100个数和第2023$个数.
(2)在前$2024$个数中,正数和负数分别有多少个？
(3)$2025$是否在这一列数中？若在,请写出它是第几个数；若不在,请说明理由.

答案： 解:
(1)由所给数列的排列规律可知,正负数相间排列,除符号外的数字依次加1,且第1个数是-1,所以这一列数中的第100个数是+100,第2023个数是-2023.
(2)因为这列数是正负数相间排列,且第1个数是负数,所以前2024个数中,正数有1012个,负数有1012个.
(3)2025不在这一列数中.因为所有排在奇数位的数都是负数,所以第2025个数是-2025.故2025不在这一列数中.