《2025年全科王同步课时练习七年级数学上册人教版》

12. 小文在做多项式减法运算时,将减去$2a^{2}+3a - 5误认为是加上2a^{2}+3a - 5$,求得的答案是$a^{2}+a - 4$(其他运算无误),那么正确的结果是(D)
A.$-a^{2}-2a + 1$
B.$-3a^{2}+a - 4$
C.$a^{2}+a - 4$
D.$-3a^{2}-5a + 6$

答案： D[提示:设原多项式为A,则A+2a²+3a-5=a²+a-4,故A=a²+a-4-(2a²+3a-5)=a²+a-4-2a²-3a+5=-a²-2a+1,则-a²-2a+1-(2a²+3a-5)=-a²-2a+1-2a²-3a+5=-3a²-5a+6.]

13. (2024·湖北十堰期中)若代数式$x^{2}+ax-(bx^{2}-x - 3)的值与字母x$无关,则$a - b$的值为(-2)
A.0
B.$-2$
C.2
D.1

答案： B[提示:因为x²+ax-(bx²-x-3)=x²+ax-bx²+x+3=(1-b)x²+(a+1)x+3,且代数式的值与字母x无关,所以1-b=0,a+1=0,解得a=-1,b=1,则a-b=-1-1=-2.]

14. (2024·河北廊坊固安县期末)若$m$,$n$互为相反数,则$(-3m - n)-2(-3m - 2n + 1)$的值为(A)
A.$-2$
B.3
C.1
D.4

答案： A[提示:(-3m-n)-2(-3m-2n+1)=-3m-n+6m+4n-2=3m+3n-2,因为m,n互为相反数,所以m+n=0,所以原式=3(m+n)-2=3×0-2=-2.]

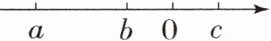
15. 有理数$a$,$b$,$c$在数轴上的对应点如图,化简$\vert a - b\vert+\vert a + b\vert-2\vert c - a\vert=$-2c.

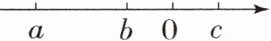
答案： -2c[提示:从数轴可知a＜b＜0＜c,所以|a-b|+|a+b|-2|c-a|=b-a-a-b-2(c-a)=b-a-a-b-2c+2a=-2c.]

16. (2024·河南许昌禹州市期中)下面是小宇同学进行整式化简的过程,请认真阅读并完成相应任务.
$6ab^{2}-ab - 2(5ab - 3ab^{2})$
$=6ab^{2}-ab-(10ab - 6ab^{2})………$第一步
$=6ab^{2}-ab - 10ab - 6ab^{2}…………$第二步
$=6ab^{2}-6ab^{2}-ab - 10ab…………$第三步
$=-11ab$. …………………………$$第四步
任务一：
①以上化简步骤中,第一步的依据是乘法分配律；
②以上化简步骤中,从第二步开始出现错误,错误的原因是去括号时没变号；
任务二：
请你写出该整式正确的化简过程,并求当$a = 3$,$b = - 2$时该整式的值.
任务二：6ab²-ab-2(5ab-3ab²)=6ab²-ab-(10ab-6ab²)=6ab²-ab-10ab+6ab²=6ab²+6ab²-ab-10ab=12ab²-11ab，当a=3,b=-2时，原式=12×3×(-2)²-11×3×(-2)=210.

答案： 任务一：①乘法分配律；②二，去括号时没变号；任务二：6ab²-ab-2(5ab-3ab²)=6ab²-ab-(10ab-6ab²)=6ab²-ab-10ab+6ab²=6ab²+6ab²-ab-10ab=12ab²-11ab，当a=3,b=-2时，原式=12×3×(-2)²-11×3×(-2)=210.

17. 小刚同学做一道题：“已知两个多项式$A$,$B$,计算$2A + B$. ”小刚同学误将$2A + B看作2A - B$,求得结果是$4xy - x - 4y + 1$；若多项式$A = x^{2}+xy - 2y$.
(1)请你帮助小刚同学求出$2A + B$的正确答案.
(2)若$2A - B的值与x$的取值无关,求$y$的值.

答案：
(1)因为2A-B=4xy-x-4y+1,A=x²+xy-2y,所以B=2(x²+xy-2y)-(4xy-x-4y+1)=2x²+2xy-4y-4xy+x+4y-1=2x²-2xy+x-1,所以2A+B=2(x²+xy-2y)+(2x²-2xy+x-1)=2x²+2xy-4y+2x²-2xy+x-1=4x²-4y+x-1.
(2)若2A-B的值与x的取值无关,即4xy-x-4y+1的值与x的取值无关,因为4xy-x-4y+1=(4y-1)x-4y+1,所以4y-1=0,解得y=$\frac{1}{4}$.

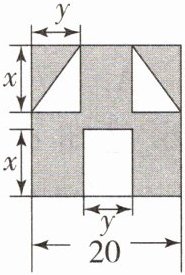
18. “囧”是网络流行语,像一个人郁闷的神情,如图,一张边长为20的正方形纸片,减去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分). 设减去的小长方形的长和宽分别为$x$,$y$,减去的两个小直角三角形的两直角边的长也分别为$x$,$y$.
(1)用含有$x$,$y$的代数式表示图中“囧”的面积(阴影部分)；
(2)当$y = \frac{5}{8}$,$x = 4$时,求此时“囧”的面积.

答案：
(1)由图得,图中“囧”的面积是20×20-$\frac{xy}{2}$×2-xy=400-xy-xy=400-2xy,即图中“囧”的面积是400-2xy.
(2)当y=$\frac{5}{8}$,x=4时,400-2xy=400-2×4×$\frac{5}{8}$=400-5=395.此时“囧”的面积是395.