第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. (2024·山东济南章丘区期中)已知$|x| = 2$,$y$是3的相反数,则$xy$的值为(
A.-1
B.-5
C.6或-6
D.-5或1
C
)A.-1
B.-5
C.6或-6
D.-5或1
答案:
C[提示:因为$|x|=2$,y 是3 的相反数,所以$x=2$或-2,y$=-3$,所以$xy=6$或-6.]
11. 有理数$a$,$b$在数轴上的位置如图所示,则下列结论中正确的是(
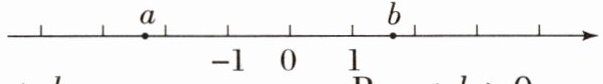
A.$a > b$
B.$a + b > 0$
C.$ab < 0$
D.$|a| < |b|$
C
)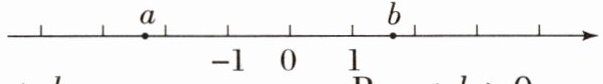
A.$a > b$
B.$a + b > 0$
C.$ab < 0$
D.$|a| < |b|$
答案:
C
12. (易错题)下列说法中正确的有(
①0乘任何数都得0;
②一个数同1相乘,仍得原数;
③-1乘任何有理数都等于这个数的相反数;
④互为相反数的两个数相乘,积是1.
A.1个
B.2个
C.3个
D.4个
C
)①0乘任何数都得0;
②一个数同1相乘,仍得原数;
③-1乘任何有理数都等于这个数的相反数;
④互为相反数的两个数相乘,积是1.
A.1个
B.2个
C.3个
D.4个
答案:
C
13. 在数-6,2,-3,5,-2中任取三个数相乘,其中最小的积是$a$,最大的积是$b$,则$a + b$ =
30
.
答案:
30[提示:任取三个数相乘,其中最大的积必须是正数,即b$=(-6)×(-3)×5=90$;最小的积为负数,即$a=(-6)$$×2×5=-60$.所以$a+b=-60+90=30.]$
14. 在1,-2,3,-4,-5,6这几个数中,任意两数之积的最大值是
20
.
答案:
20
15. 按如图所示的程序计算,如果输入的数是-6,那么输出的数是______.
]

]

162
答案:
162[提示:若输入的数是-6,则$(-6)×(-3)=18,|18|$$<100$,则$18×(-3)=-54,|-54|<100,(-54)×$$(-3)=162,|162|>100$,所以输出162.]
16. 在计算$\left(-9\frac{1}{2}\right)× \left(-8\frac{2}{3}\right)$时,小明是这样做的:
$\left(-9\frac{1}{2}\right)× \left(-8\frac{2}{3}\right)$
$=9\frac{1}{2}× 8\frac{2}{3}$(第一步)
$=3× 8$(第二步)
$=24$(第三步).
他的计算对吗?如果不对,是从哪一步开始出错的?把它改正过来.
$\left(-9\frac{1}{2}\right)× \left(-8\frac{2}{3}\right)$
$=9\frac{1}{2}× 8\frac{2}{3}$(第一步)
$=3× 8$(第二步)
$=24$(第三步).
他的计算对吗?如果不对,是从哪一步开始出错的?把它改正过来.
答案:
解:不对,从第二步开始出现错误.原式$=9\frac {1}{2}×8\frac {2}{3}=\frac {19}{2}×\frac {26}{3}=\frac {247}{3}.$
17. 若定义一种新的运算“*”,规定$A*B = 4AB$,如$2*3 = 4× 2× 3 = 24$.
(1)求$3*(-4)$的值;
(2)求$(-2)*(6*3)$的值.
(1)求$3*(-4)$的值;
(2)求$(-2)*(6*3)$的值.
答案:
解:
(1)$3*(-4)=4×3×(-4)=-48.$
(2)$(-2)*(6*3)=(-2)*(4×6×3)=(-2)*72=4×(-2)×72=-576.$
(1)$3*(-4)=4×3×(-4)=-48.$
(2)$(-2)*(6*3)=(-2)*(4×6×3)=(-2)*72=4×(-2)×72=-576.$
18. 已知$a$,$b$为有理数,现规定一种新运算$\oplus$,满足$a\oplus b = a× b - a$.
(1)求$(-2)\oplus 4$的值.
(2)求$(1\oplus 4)\oplus \left(-2\frac{1}{2}\right)$的值.
(3)新运算$a\oplus b = a× b - a$是否满足加法交换律?若满足,请说明理由;若不满足,请举出一个反例.
(1)求$(-2)\oplus 4$的值.
(2)求$(1\oplus 4)\oplus \left(-2\frac{1}{2}\right)$的值.
(3)新运算$a\oplus b = a× b - a$是否满足加法交换律?若满足,请说明理由;若不满足,请举出一个反例.
答案:
解:
(1)$(-2)\oplus 4=(-2)×4-(-2)=-6.$
(2)因为1$\oplus 4=1×4-1=3$,所以$(1\oplus 4)\oplus (-2\frac {1}{2})=3\oplus (-2\frac {1}{2})=3×(-2\frac {1}{2})-3=-\frac {21}{2}.$
(3)不满足加法交换律.如:$(-2)\oplus 4=(-2)×4-(-2)=-6,4\oplus (-2)=4×(-2)-4=-12$.以上两式不相等,故不满足加法交换律.
(1)$(-2)\oplus 4=(-2)×4-(-2)=-6.$
(2)因为1$\oplus 4=1×4-1=3$,所以$(1\oplus 4)\oplus (-2\frac {1}{2})=3\oplus (-2\frac {1}{2})=3×(-2\frac {1}{2})-3=-\frac {21}{2}.$
(3)不满足加法交换律.如:$(-2)\oplus 4=(-2)×4-(-2)=-6,4\oplus (-2)=4×(-2)-4=-12$.以上两式不相等,故不满足加法交换律.
查看更多完整答案,请扫码查看


