《2025年全科王同步课时练习七年级数学上册人教版》

11. (易错题)下列等式中,$x$,$y$这两个量成反比例关系的是(D)
A.$x + y = 15$
B.$y = 7x$
C.$x:2 = y:3$
D.$x:2 = 3:y$

答案： D[提示:A中,x+y=15,是和一定,则x和y不成比例.B中,y=7x,即y:x=7,是比值一定,则x和y成正比例.C中,x:2=y:3,即$x:y=\frac{2}{3}$是比值一定,则x和y成正比例.D中,x:2=3:y,即xy=6,是乘积一定,则x和y成反比例.]

12. 下列问题中变量之间的关系是正比例关系的是(C)
A.总价一定时,单价与数量之间的关系
B.用 $10m$长的绳子围一个长方形,所围成的长方形的长 $y(m)$与宽 $x(m)$之间的关系
C.一场电影的票价一定时,该场电影的票房收入 $m$(元)与出售票数 $n$(张)之间的关系
D.三角形的面积一定时,底边的长度 $y$与对应的高的长度 $x$之间的关系

答案： D[提示:正比例关系的一般式为y=kx(k≠0).因为单价×数量=总价,即单价=$\frac{总价}{数量}$,则总价一定,单价是数量的反比例关系,故A不符合要求.因为2×(x+y)=10,即y=-x+5,所以y与x不是正比例关系,故B不符合要求.令一张电影票的价钱为a元,则m=an,显然a为定值且不等于0,所以m与n成正比例关系,故C符合要求.因为$S=\frac{xy}{2}$,即xy=2S,所以S一定时,y与x成反比例关系,故D不符合要求.]

13. (2024·上海奉贤区期中)下列问题中的两个变量成反比例关系的是(A)
A.被除数(不为零)一定,除数与商
B.货物的单价一定,货物的总价与货物的数量
C.等腰三角形的周长一定,它的腰长与底边的长
D.汽车所行的速度一定,它所行驶的路程与时间

答案： A[提示:A中,被除数(不为零)一定,除数与商是反比例关系;B中,货物的单价一定,货物的总价与货物的数量是正比例关系;C中,等腰三角形的周长一定,它的腰长与底边的长不是反比例关系;D中,汽车所行的速度一定,它所行驶的路程与时间是正比例关系.]

14. (2024·江苏泰兴市二模)在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强如下表：

则可以反映 $p$与 $V$之间的关系的式子是(D)
A.$p = 3000V$
B.$p = 6000V$
C.$pV = 3000$
D.$pV = 6000$

答案： D

15. 如图,小华设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点 $O$左侧固定位置 $B$处悬挂重物 $A$,在中点 $O$右侧用一个弹簧秤向下拉,改变弹簧秤与点 $O$的距离 $x(cm)$,观察弹簧秤的示数 $y(N)$的变化情况。实验数据记录如下：


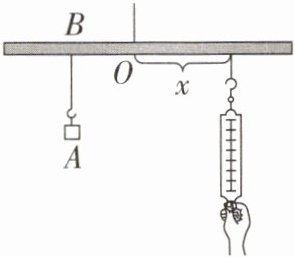
猜测 $y$与 $x$之间的关系,并写出关系为xy=300。

答案： xy=300[提示:由表格猜测y与x之间的关系为反比例关系,设xy=k(k≠0).把x=10,y=30代入得k=300,所以xy=300.将其余各组数据代入验证均符合.所以y与x的关系为xy=300.]

16. 若长方形的两邻边长度分别为 $x$,$y$,面积保持不变,下表给出了 $x$与 $y$的一些值求长方形面积。
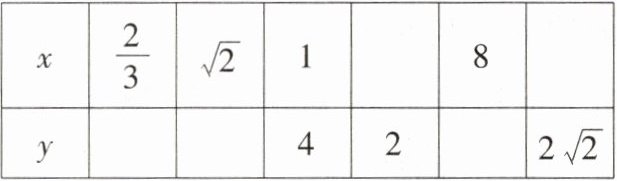
(1)$xy=4$请你根据表格信息写出 $y$与 $x$之间的关系式；
(2)$\begin{array}{|c|c|c|c|c|c|c|}\hline x&\frac{2}{3}&\sqrt{2}&1&2&8&2\sqrt{2}\\\hline y&6&2\sqrt{2}&4&2&\frac{1}{2}&\sqrt{2}\\\hline\end{array}$根据关系式完成下表。

答案： 解:
(1)设xy=k,由于(1,4)满足此关系,因此k=1×4=4,所以xy=4.
(2)$4÷\frac{2}{3}=4×\frac{3}{2}=6$,$\frac{4}{\sqrt{2}}=2\sqrt{2}$,4÷2=2,$\frac{4}{8}=\frac{1}{2}$,$\frac{4}{2\sqrt{2}}=\sqrt{2}$.所以表格如下:
$\begin{array}{|c|c|c|c|c|c|c|}\hline x&\frac{2}{3}&\sqrt{2}&1&2&8&\sqrt{2}\\\hline y&6&2\sqrt{2}&4&2&\frac{1}{2}&2\sqrt{2}\\\hline\end{array}$

17. 已知圆锥的体积 $V= \frac{1}{3}Sh$,其中 $S$表示圆锥的底面积,$h$表示圆锥的高。若圆锥的体积不变,当 $h$为 $10cm$时,底面积为 $30cm^{2}$,请写出 $h$与 $S$的关系。

答案： 解:因为$V=\frac{1}{3}Sh$,当h为10cm时,底面积为30cm²,所以$V=\frac{1}{3}×10×30=100(cm^3)$,所以$100=\frac{1}{3}Sh$,所以h与S的关系为Sh=300.