《2025年全科王同步课时练习七年级数学上册人教版》

1. 如图,数轴上的点A,B,C分别表示有理数a,b,c.

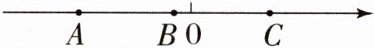
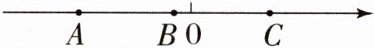
(1) 比较大小：$a - b$＜0,$a + c$＜0,$c - b$＞0.(填“＞”“＜”或“=”)
(2) 化简：$\vert a - b\vert - \vert a + c\vert + \vert c - b\vert$.
解:|a-b|-|a+c|+|c-b|=b-a+a+c+c-b=2c.

答案： 1.
(1)＜ ＜ ＞[提示:根据数轴可得a＜b＜0＜c,且|b|＜|c|＜|a|,所以a-b＜0,a+c＜0,c-b＞0.]
(2)解:|a-b|-|a+c|+|c-b|=b-a+a+c+c-b=2c.

二 根据绝对值的性质求值
2. (2024·山东滨州阳信县期中)当$x = a$时,式子$\vert x - 1\vert + 10$有最小值b,则$a + b$的值为______11.
3. 若$\vert a\vert = 19$,$\vert b\vert = 97$,且$\vert a + b\vert = \vert a\vert + \vert b\vert$,求$a + b$的值.
解:因为|a|=19,|b|=97,所以a=±19,b=±97.又因为|a+b|=|a|+|b|,所以a=19,b=97或a=-19,b=-97.所以a+b=116或-116.
4. 已知$\vert ab - 2\vert与\vert b - 1\vert$互为相反数,求$\frac{1}{ab} + \frac{1}{(a + 1)(b + 1)} + \frac{1}{(a + 2)(b + 2)} + … + \frac{1}{(a + 2022)(b + 2022)}$的值.
解:根据题意可知|ab-2|+|b-1|=0,所以|ab-2|=0,|b-1|=0,即ab=2,b=1,所以a=2.所以$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}+\cdots+\frac{1}{(a+2022)(b+2022)}=\frac{1}{1×2}+\frac{1}{2×3}+\cdots+\frac{1}{2023×2024}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2023}-\frac{1}{2024}=1-\frac{1}{2024}=\frac{2023}{2024}$.

答案： 2.11[提示:因为式子|x-1|+10有最小值b,所以x-1=0,b=10,解得x=1,故a=1,则a+b=11.] 3.解:因为|a|=19,|b|=97,所以a=±19,b=±97.又因为|a+b|=|a|+|b|,所以a=19,b=97或a=-19,b=-97.所以a+b=116或-116. 4.解:根据题意可知|ab-2|+|b-1|=0,所以|ab-2|=0,|b-1|=0,即ab=2,b=1,所以a=2.所以$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}+\cdots+\frac{1}{(a+2022)(b+2022)}=\frac{1}{1×2}+\frac{1}{2×3}+\cdots+\frac{1}{2023×2024}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2023}-\frac{1}{2024}=1-\frac{1}{2024}=\frac{2023}{2024}$.

三 根据绝对值的性质解决$\frac{\vert ab\vert}{-ab}$型问题
5. 若$\frac{a}{\vert a\vert} + \frac{b}{\vert b\vert} = 0$,则$\frac{\vert ab\vert}{-ab} = $1.
6. 分类讨论是一种重要的数学方法,如在化简$\vert a\vert$时,可以这样分类：当$a ＞ 0$时,$\vert a\vert = a$；当$a = 0$时,$\vert a\vert = 0$；当$a ＜ 0$时,$\vert a\vert = -a$. 用这种方法解决下列问题：
(1) 当$a = 5$时,求$\frac{\vert a\vert}{a}$的值；
(2) 当$a = -2$时,求$\frac{a}{\vert a\vert}$的值；
(3) 若有理数a不等于零,求$\frac{\vert a\vert}{a}$的值；
(4) 若有理数a,b均不等于零,试求$\frac{a}{\vert a\vert} + \frac{\vert b\vert}{b}$的值.
解:
(1)当a=5时,$\frac{|a|}{a}=1$.
(2)当a=-2时,$\frac{a}{|a|}=-1$.
(3)当a＞0时,$\frac{|a|}{a}=1$,当a＜0时,$\frac{|a|}{a}=-1$.
(4)若有理数a,b均不等于零,则当a,b同为正数时,$\frac{a}{|a|}+\frac{|b|}{b}=2$;当a,b同为负数时,$\frac{a}{|a|}+\frac{|b|}{b}=-2$;当a,b异号时,$\frac{a}{|a|}+\frac{|b|}{b}=0$.
7. 已知a,b,c都不等于零,且$\frac{a}{\vert a\vert} + \frac{b}{\vert b\vert} + \frac{c}{\vert c\vert} - \frac{abc}{\vert abc\vert}$的最大值是m,最小值为n,求$\frac{n^{m}}{mn}$的值.
解:当a,b,c三个都大于0时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=2$;当a,b,c三个都小于0时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=-2$;当a,b,c一正二负时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=-2$;当a,b,c二正一负时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=2$.所以m=2,n=-2,所以原式=$\frac{(-2)^2}{2×(-2)}=-\frac{4}{4}=-1$.

答案： 5.1[提示:由$\frac{a}{|a|}+\frac{b}{|b|}=0$,得a与b异号,则$\frac{|ab|}{-ab}=1$.] 6.解:
(1)当a=5时,$\frac{|a|}{a}=1$.
(2)当a=-2时,$\frac{a}{|a|}=-1$.
(3)当a＞0时,$\frac{|a|}{a}=1$,当a＜0时,$\frac{|a|}{a}=-1$.
(4)若有理数a,b均不等于零,则当a,b同为正数时,$\frac{a}{|a|}+\frac{|b|}{b}=2$;当a,b同为负数时,$\frac{a}{|a|}+\frac{|b|}{b}=-2$;当a,b异号时,$\frac{a}{|a|}+\frac{|b|}{b}=0$. 7.解:当a,b,c三个都大于0时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=2$;当a,b,c三个都小于0时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=-2$;当a,b,c一正二负时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=-2$;当a,b,c二正一负时,可得$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}-\frac{abc}{|abc|}=2$.所以m=2,n=-2,所以原式=$\frac{(-2)^2}{2×(-2)}=-\frac{4}{4}=-1$.