第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
12. 我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量. 如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如$2513 = 2× 7^{3} + 5× 7^{2} + 1× 7^{1} + 3$)来记录孩子自出生后的天数. 由图可知,孩子自出生后的天数是(
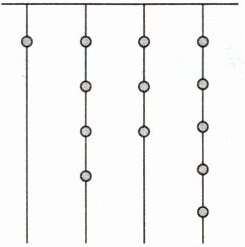
A.$1435$天
B.$565$天
C.$13$天
D.$465$天
565
)
A.$1435$天
B.$565$天
C.$13$天
D.$465$天
答案:
B[提示:由图可知:$1× 7^{3}+4× 7^{2}+3× 7^{1}+5=1× 343+4× 49+3× 7+5=343+196+21+5=565$(天).即孩子自出生后的天数是565天.]
13. 定义一种新运算:$a※b = b^{2} - ab$,如:$2※3 = 3^{2} - 2× 3 = 3$,则计算$(-1※2)※(-4)$的结果为(
A.$-3$
B.$8$
C.$15$
D.$40$
40
)A.$-3$
B.$8$
C.$15$
D.$40$
答案:
D[提示:根据题中的新定义得$(-1※2)※(-4)=[2^{2}-(-1× 2)]※(-4)=6※(-4)=(-4)^{2}-6× (-4)=16+24=40.]$
14. 若$m$,$n满足\vert m + 3\vert + (n - 2)^{2} = 0$,则$(m + n)^{2023} = $
-1
。
答案:
-1[提示:因为$|m+3|+(n-2)^{2}=0$,所以$m+3=0,n-2=0$,所以$m=-3,n=2$,所以$(-3+2)^{2023}=-1.]$
15. 观察下列等式,找出规律,然后在空格处填上具体的数字.
$1 + 3 = 4 = 2^{2}$;
$1 + 3 + 5 = 9 = 3^{2}$;
$1 + 3 + 5 + 7 = 16 = 4^{2}$;
$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$;
$1 + 3 + 5 + 7 + 9 + 11 = 36 = 6^{2}$。
根据规律填空:$1 + 3 + 5 + 7 + 9 + … + 2023 = $
$1 + 3 = 4 = 2^{2}$;
$1 + 3 + 5 = 9 = 3^{2}$;
$1 + 3 + 5 + 7 = 16 = 4^{2}$;
$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$;
$1 + 3 + 5 + 7 + 9 + 11 = 36 = 6^{2}$。
根据规律填空:$1 + 3 + 5 + 7 + 9 + … + 2023 = $
$1012^{2}$
。
答案:
$1012^{2}$[提示:根据材料可知,和的结果是首数与末数的平均数的平方.所以$1+3+5+7+9+\cdots +2023=(\frac {1+2023}{2})^{2}=1012^{2}.]$
16. 计算.
(1)$-3^{2}÷ 2\frac{1}{4}× (-\frac{1}{2})^{2} - 2× (-\frac{1}{3})$;
(2)$(\frac{1}{4} + \frac{1}{6} - \frac{1}{2})× 12 + (-2)^{3}÷ (-4)$;
(3)$3^{2} + (-2 - 5)÷ 7 - \vert -\frac{1}{4}\vert× (-2)^{4} + (-1)^{2023}$。
(1)$-3^{2}÷ 2\frac{1}{4}× (-\frac{1}{2})^{2} - 2× (-\frac{1}{3})$;
(2)$(\frac{1}{4} + \frac{1}{6} - \frac{1}{2})× 12 + (-2)^{3}÷ (-4)$;
(3)$3^{2} + (-2 - 5)÷ 7 - \vert -\frac{1}{4}\vert× (-2)^{4} + (-1)^{2023}$。
答案:
解:
(1)原式$=-9× \frac {4}{9}× \frac {1}{4}+\frac {2}{3}=-1+\frac {2}{3}=-\frac {1}{3}.$
(2)原式$=\frac {1}{4}× 12+\frac {1}{6}× 12-\frac {1}{2}× 12+(-8)÷ (-4)=3+2-6+2=1.$
(3)原式$=9+(-7)÷ 7-\frac {1}{4}× 16-1=9-1-4-1=3.$
(1)原式$=-9× \frac {4}{9}× \frac {1}{4}+\frac {2}{3}=-1+\frac {2}{3}=-\frac {1}{3}.$
(2)原式$=\frac {1}{4}× 12+\frac {1}{6}× 12-\frac {1}{2}× 12+(-8)÷ (-4)=3+2-6+2=1.$
(3)原式$=9+(-7)÷ 7-\frac {1}{4}× 16-1=9-1-4-1=3.$
17. (2024·青岛莱西市期中)观察下列各式:
$1^{3} = 1 = \frac{1}{4}× 1^{2}× 2^{2}$;
$1^{3} + 2^{3} = 9 = \frac{1}{4}× 2^{2}× 3^{2}$;
$1^{3} + 2^{3} + 3^{3} = 36 = \frac{1}{4}× 3^{2}× 4^{2}$;
$1^{3} + 2^{3} + 3^{3} + 4^{3} = 100 = \frac{1}{4}× 4^{2}× 5^{2}$。
用你发现的规律解答下面的问题:
(1)$1^{3} + 2^{3} + 3^{3} + … + 19^{3} + 20^{3}$;
(2)$10^{3} + 11^{3} + 12^{3} + … + 19^{3} + 20^{3}$。
$1^{3} = 1 = \frac{1}{4}× 1^{2}× 2^{2}$;
$1^{3} + 2^{3} = 9 = \frac{1}{4}× 2^{2}× 3^{2}$;
$1^{3} + 2^{3} + 3^{3} = 36 = \frac{1}{4}× 3^{2}× 4^{2}$;
$1^{3} + 2^{3} + 3^{3} + 4^{3} = 100 = \frac{1}{4}× 4^{2}× 5^{2}$。
用你发现的规律解答下面的问题:
(1)$1^{3} + 2^{3} + 3^{3} + … + 19^{3} + 20^{3}$;
(2)$10^{3} + 11^{3} + 12^{3} + … + 19^{3} + 20^{3}$。
答案:
解:
(1)$1^{3}+2^{3}+3^{3}+\cdots +19^{3}+20^{3}=\frac {1}{4}× 20^{2}× 21^{2}=\frac {1}{4}× 400× 441=44100.$
(2)$10^{3}+11^{3}+12^{3}+\cdots +19^{3}+20^{3}=(1^{3}+2^{3}+3^{3}+\cdots +20^{3})-(1^{3}+2^{3}+3^{3}+\cdots +9^{3})=44100-\frac {1}{4}× 9^{2}× 10^{2}=44100-2025=42075.$
(1)$1^{3}+2^{3}+3^{3}+\cdots +19^{3}+20^{3}=\frac {1}{4}× 20^{2}× 21^{2}=\frac {1}{4}× 400× 441=44100.$
(2)$10^{3}+11^{3}+12^{3}+\cdots +19^{3}+20^{3}=(1^{3}+2^{3}+3^{3}+\cdots +20^{3})-(1^{3}+2^{3}+3^{3}+\cdots +9^{3})=44100-\frac {1}{4}× 9^{2}× 10^{2}=44100-2025=42075.$
查看更多完整答案,请扫码查看


