《2025年全科王同步课时练习七年级数学上册人教版》

11. (2024·河北廊坊广阳区期末)一个两位数,个位上的数字为m,十位上的数字为n,如果在它们之间添上一个0,就得到一个三位数,用代数式表示这个三位数为 (B)
A.$10n + m$
B.$100n + m$
C.$nm$
D.$100m + n$

答案： B[提示:由题意可知,这个三位数的百位上的数字为n,十位上的数字为0,个位上的数字为m,所以这个三位数是100n+m.]

12. 读书使人聪颖智慧,小亮先用m天读完一部书籍的上集,又用n天读完下集,这部书籍上下集共100万字,小亮平均每天的阅读量为$\frac{100}{m+n}$万字.

答案： $\frac{100}{m+n}$[提示:因为小亮先用m天阅读了书籍的上集,又用n天阅读了书籍的下集,这部书籍上下集共100万字,所以小亮平均每天的阅读量为$\frac{100}{m+n}$万字.]

13. 如图,某餐桌桌面可由圆形折叠成正方形(图中阴影表示可折叠部分).若折叠前圆形桌面的直径为a m.折叠成正方形后其边长为b m,则桌面可折叠部分的面积为$\frac{\pi a^2}{4}-b^2$$m^{2}$.(用含a,b的式子表示)

答案： ($\frac{\pi a^2}{4}-b^2$)

14. 如图所示的四个图形是由小花“”摆成的一组有规律的图案,按图中规律,第n个图形中小花的朵数是(2n-1)(n+1).
(1) (2) (3) (4)

答案： (2n-1)(n+1)[提示:第一个图形小花朵数是1×2,第二个图形小花朵数是3×3,第三个图形小花朵数是5×4,第四个图形小花朵数是7×5,…,则第n个图形小花朵数是(2n-1)(n+1).]

15. 某公司以每吨200元的价格购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表：

现将该矿石原料全部用完.设生产甲产品x吨,用含x的式子表示乙产品的吨数.

答案： 解:因为生产1吨甲产品需要的矿石原料为10吨,所以生产甲产品x吨需要的矿石原料为10x吨,所以生产乙产品的矿石原料为(300-10x)吨.因为生产1吨乙产品需要矿石4吨,所以乙产品的吨数为$\frac{300-10x}{4}$,所以用含x的式子表示乙产品的吨数为$\frac{300-10x}{4}$.

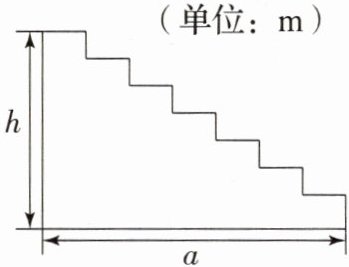
16. 一座楼梯的示意图如图所示,现要在楼梯上铺一条地毯.
(1)需要多长的地毯?
(2)如果楼梯的宽为b,那么地毯的面积为多少?
(单位：m)

答案： 解:
(1)由题意,得地毯的长度为(a+h)m.
(2)地毯的面积为(a+h)b$m^2$.

17. 将黑色圆点按如图所示的规律进行排列：

图中黑色圆点的个数依次为:1,3,6,10,….将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为1275.

答案： 1275[提示:第①个图形中的黑色圆点的个数为1,第②个图形中的黑色圆点的个数为$\frac{(1+2)×2}{2}=3$,第③个图形中的黑色圆点的个数为$\frac{(1+3)×3}{2}=6$,第④个图形中的黑色圆点的个数为$\frac{(1+4)×4}{2}=10$,…,第ⓝ个图形中的黑色圆点的个数为$\frac{n(n+1)}{2}$,则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,…,其中每3个数中,都有2个能被3整除.33÷2=16……1,16×3+2=50,则第33个被3整除的数为原数列中第50个数,即$\frac{50×51}{2}=1275$.]