第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. (2023·北京海淀区月考)下列比较大小正确的是(
A.$ -\dfrac{5}{6} < -\dfrac{4}{5} $
B.$ -(-21) < +(-21) $
C.$ -\left\vert -10\dfrac{1}{2}\right\vert > 8\dfrac{2}{3} $
D.$ -\left\vert -7\dfrac{2}{3}\right\vert > -\left(-7\dfrac{2}{3}\right) $
A
)A.$ -\dfrac{5}{6} < -\dfrac{4}{5} $
B.$ -(-21) < +(-21) $
C.$ -\left\vert -10\dfrac{1}{2}\right\vert > 8\dfrac{2}{3} $
D.$ -\left\vert -7\dfrac{2}{3}\right\vert > -\left(-7\dfrac{2}{3}\right) $
答案:
A[提示:A中,因为$\left$|$-\frac{5}{6}\right$|$=\frac{5}{6},\left$|$-\frac{4}{5}\right$|$=\frac{4}{5},\frac{5}{6}>\frac{4}{5},$所以$-\frac{5}{6}$<-\frac{4}{5}. B中,-(-21)=21,+(-21)=-21,所以-(-21)>+(-21). C中,因为$-\left$|$-10\frac{1}{2}\right$|$=-10\frac{1}{2},$所以$-\left$|$-10\frac{1}{2}\right$|<8\frac{2}{3}. D中,因为$-\left$|$-7\frac{2}{3}\right$|$=-7\frac{2}{3},-\left(-7\frac{2}{3}\right)=7\frac{2}{3},$所以$-\left$|$-7\frac{2}{3}\right$|<-\left(-7\frac{2}{3}\right).
11. (易错题)有理数m,n在数轴上对应点的位置如图,则m,n,$ \vert n \vert $,$ -m $,0的大小关系是(
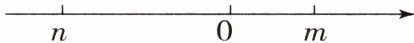
A.$ n < 0 < -m < m < \vert n \vert $
B.$ n < -m < 0 < \vert n \vert < m $
C.$ n < \vert n \vert < 0 < -m < m $
D.$ n < -m < 0 < m < \vert n \vert $
D
)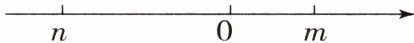
A.$ n < 0 < -m < m < \vert n \vert $
B.$ n < -m < 0 < \vert n \vert < m $
C.$ n < \vert n \vert < 0 < -m < m $
D.$ n < -m < 0 < m < \vert n \vert $
答案:
D[提示:根据有理数m,n在数轴上对应点的位置得n<0 <m,且$|n|>m$.所以有理数n,−m,m,$|n|$在数轴上的位置如图,所以n<−m<0<m<$|n|$.]
12. 下列说法不正确的是(
A.若$ a > b > 0 $,则$ \vert a \vert > \vert b \vert $
B.若$ \vert -a \vert > \vert -b \vert $,则$ \vert a \vert > \vert b \vert $
C.若a为有理数,则$ \vert a \vert > 0 $
D.若a为有理数,则$ \vert a \vert \geq 0 $
C
)A.若$ a > b > 0 $,则$ \vert a \vert > \vert b \vert $
B.若$ \vert -a \vert > \vert -b \vert $,则$ \vert a \vert > \vert b \vert $
C.若a为有理数,则$ \vert a \vert > 0 $
D.若a为有理数,则$ \vert a \vert \geq 0 $
答案:
C[提示:两个正数,一个数越大,绝对值越大,故选项A正确.互为相反数的两个数的绝对值相等,所以一个数的绝对值大于另一个数的绝对值,则这个数的相反数的绝对值也大于另一个数的相反数的绝对值,故选项B正确.若a为有理数,则$|a|\geq0$,故选项C错误,选项D正确.]
13. 比较下列各组数的大小.
(1)$ -(-1) $
(2)$ -\dfrac{8}{21} $
(3)$ -(-0.3) $
(4)$ -\vert -2 \vert $
(1)$ -(-1) $
>
$ -(+2) $;(2)$ -\dfrac{8}{21} $
>
$ -\dfrac{3}{7} $;(3)$ -(-0.3) $
<
$ \left\vert -\dfrac{1}{3}\right\vert $;(4)$ -\vert -2 \vert $
<
$ -(-2) $.
答案:
(1)>
(2)>
(3)<
(4)<
(1)>
(2)>
(3)<
(4)<
14. 按要求完成下列各题.
(1)在数轴上表示出0,$ -2 $,3,$ -\dfrac{1}{2} $;
(2)将(1)中各数用“<”连接起来;
(3)将(1)中各数的相反数用“<”连接起来;
(4)将(1)中各数的绝对值用“<”连接起来.
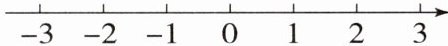
(1)在数轴上表示出0,$ -2 $,3,$ -\dfrac{1}{2} $;
(2)将(1)中各数用“<”连接起来;
(3)将(1)中各数的相反数用“<”连接起来;
(4)将(1)中各数的绝对值用“<”连接起来.
答案:
解:
(1)如图.
(2)−2<−$\frac{1}{2}$<0<3.
(3)−3<0<$\frac{1}{2}$<2.
(4)$|0|$<$\left|-\frac{1}{2}\right|$<$|-2|$<$|3|$.
解:
(1)如图.
(2)−2<−$\frac{1}{2}$<0<3.
(3)−3<0<$\frac{1}{2}$<2.
(4)$|0|$<$\left|-\frac{1}{2}\right|$<$|-2|$<$|3|$.

15. 有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了4个单位长度到达点C处,蚂蚁乙从图中点B的位置沿数轴向左爬了8个单位长度到达点D处.
(1)在图中描出点C,D的位置;
(2)点E到点C与点D的距离相等,在数轴上描出点E的位置,并用“<”把点A,B,C,D,E所表示的数连接起来.
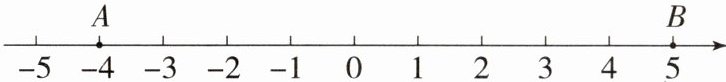
(1)在图中描出点C,D的位置;
(2)点E到点C与点D的距离相等,在数轴上描出点E的位置,并用“<”把点A,B,C,D,E所表示的数连接起来.
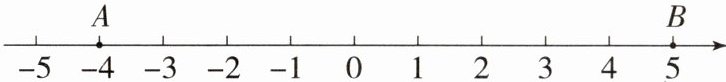
答案:
解:
(1)由题意得,C点表示的数为0,D点表示的数为−3.在数轴上描出C,D的位置如图
(1).
(2)易知点E表示的数是−1.5,在数轴上描出点E的位置如图
(2),用“<"把点A,B,C,D,E所表示的数连接起来为−4<−3<−1.5<0<5.
解:
(1)由题意得,C点表示的数为0,D点表示的数为−3.在数轴上描出C,D的位置如图
(1).
(2)易知点E表示的数是−1.5,在数轴上描出点E的位置如图
(2),用“<"把点A,B,C,D,E所表示的数连接起来为−4<−3<−1.5<0<5.

16. (1)当$ a > 0 $时,a
当$ a = 0 $时,a
当$ a < 0 $时,a
(2)请仿照(1)的方法,比较2a和a的大小.
>
-a;当$ a = 0 $时,a
=
-a;当$ a < 0 $时,a
<
-a.(2)请仿照(1)的方法,比较2a和a的大小.
解:当a>0时,2a>a;当a=0时,2a=a;当a<0时,2a<a.
答案:
解:
(1)当a>0时,a>−a;当a=0时,a=−a;当a<0 时,a<−a.
(2)当a>0时,2a>a;当a=0时,2a=a;当a<0时,2a<a.
(1)当a>0时,a>−a;当a=0时,a=−a;当a<0 时,a<−a.
(2)当a>0时,2a>a;当a=0时,2a=a;当a<0时,2a<a.
查看更多完整答案,请扫码查看


