第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2024·安徽天长市期中)观察下列关于$x$的单项式,探究其规律:$-2x$,$4x^{2}$,$-6x^{3}$,$8x^{4}$,$-10x^{5}$,$12x^{6}$,…$$,按照上述规律,第$2023$个单项式是(
A.$-4046x^{2022}$
B.$4046x^{2022}$
C.$-4046x^{2023}$
D.$4046x^{2023}$
$-4046x^{2023}$
)A.$-4046x^{2022}$
B.$4046x^{2022}$
C.$-4046x^{2023}$
D.$4046x^{2023}$
答案:
C[提示:根据所给单项式发现奇数个单项式的系数为负,偶数个单项式的系数为正,第n个单项式系数的绝对值是2n,指数是n,即公式为$2n\cdot (-x)^{n}$,所以第2023个单项式是$-4046x^{2023}$.]
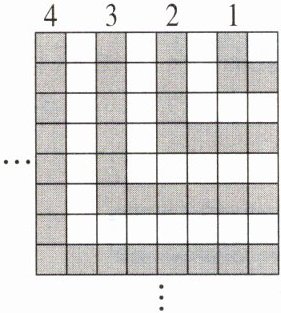
2. (2024·广东河源连平县期末)将正整数按如图所示的方式排列,根据图中的规律,$20$应在(
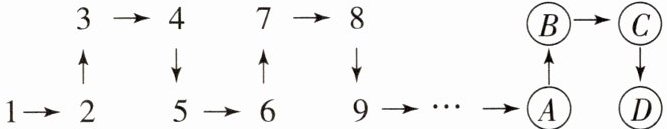
A.$A$位
B.$B$位
C.$C$位
D.$D$位
C
)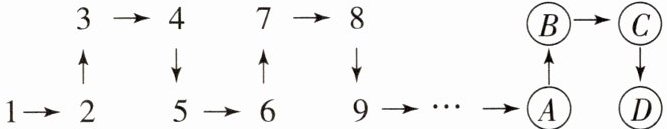
A.$A$位
B.$B$位
C.$C$位
D.$D$位
答案:
C[提示:被4除余数是1的排在D位,被4除余数是2的排在A位,被4除余数是3的排在B位,被4整除的排在C位.$20÷4=5$,所以20应在C位.]
3. 图(1)为全体奇数排成的数表,用十字框任意圈出$5$个数,记框内中间这个数为$a$(如图(2)所示)。
(1)请用含$a的式子表示框内的其余4$个数。
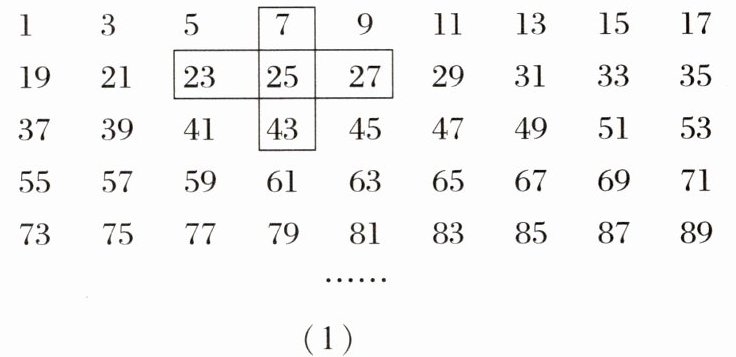
(2)框内的$5个数之和能等于2015$,$2020$吗?若不能,请说明理由;若能,请求出这$5$个数中最小的一个数。
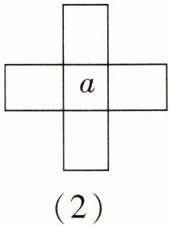
(1)请用含$a的式子表示框内的其余4$个数。

(2)框内的$5个数之和能等于2015$,$2020$吗?若不能,请说明理由;若能,请求出这$5$个数中最小的一个数。

答案:
(1)由题意,中间的数是a,则a的上面一个数为a-18,下面一个数为a+18,前面一个数为a-2,后面一个数为a+2.
(2)设中间的数是a,依题意有5a=2015,a=403,符合题意,这5个数中最小的一个数是a-18=403-18=385.5a=2020,a=404,404是偶数,不合题意,舍去.即十字框内的5个数之和不能等于2020,能等于2015.
(1)由题意,中间的数是a,则a的上面一个数为a-18,下面一个数为a+18,前面一个数为a-2,后面一个数为a+2.
(2)设中间的数是a,依题意有5a=2015,a=403,符合题意,这5个数中最小的一个数是a-18=403-18=385.5a=2020,a=404,404是偶数,不合题意,舍去.即十字框内的5个数之和不能等于2020,能等于2015.
4. (2023·重庆中考)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了$9$根木棍,第②个图案用了$14$根木棍,第③个图案用了$19$根木棍,第④个图案用了$24$根木棍,…$$,按此规律排列下去,则第⑧个图案用的木棍根数是(

A.$39$
B.$44$
C.$49$
D.$54$
B
)
A.$39$
B.$44$
C.$49$
D.$54$
答案:
B[提示:由图得,第①个图案有4+5=9根木棍,第②个图案有4+5×2=14根木棍,第③个图案有4+5×3=19根木棍,…,所以第n个图案有(4+5n)根木棍,所以第⑧个图案有4+5×8=44根木棍.]
5. 观察如图所示的图案,它们都是由边长为$1cm$的小正方形按一定规律拼接而成的,依此规律,则第$9$个图案中的小正方形有
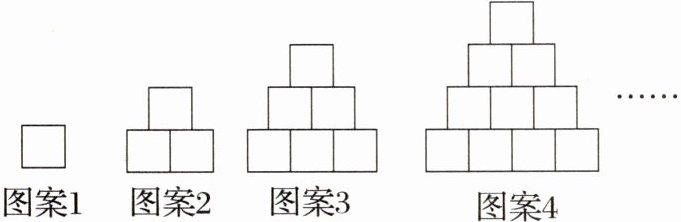
45
个。
答案:
45[提示:设第n个图案有$a_{n}$个小正方形(n为正整数),观察图形,可知$a_{1}=1$,$a_{2}=1+2=3$,$a_{3}=1+2+3=6$,$a_{4}=1+2+3+4=10$,…,所以$a_{n}=1+2+3+\cdots +n=\frac{n(n+1)}{2}$(n为正整数),所以$a_{9}=\frac{9× (9+1)}{2}=45$.]
6. 如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第$1个黑色L形由3$个正方形组成,第$2个黑色L形由7$个正方形组成,依次按这样的规律镶嵌。
(1)求第$7个黑色L$形的正方形个数;
(2)求第$n个黑色L$形的正方形个数。
(1)求第$7个黑色L$形的正方形个数;
(2)求第$n个黑色L$形的正方形个数。

答案:
(1)第1个黑色L形由3个正方形组成,第2个黑色L形由3+4=7个正方形组成,第3个黑色L形由3+2×4=11个正方形组成,…,所以组成第7个黑色L形的正方形个数是3+(7-1)×4=27.
(2)第1个黑色L形由3个正方形组成,第2个黑色L形由3+4=7个正方形组成,第3个黑色L形由3+2×4=11个正方形组成,…,所以组成第n个黑色L形的正方形个数是3+(n-1)×4=4n-1.
(1)第1个黑色L形由3个正方形组成,第2个黑色L形由3+4=7个正方形组成,第3个黑色L形由3+2×4=11个正方形组成,…,所以组成第7个黑色L形的正方形个数是3+(7-1)×4=27.
(2)第1个黑色L形由3个正方形组成,第2个黑色L形由3+4=7个正方形组成,第3个黑色L形由3+2×4=11个正方形组成,…,所以组成第n个黑色L形的正方形个数是3+(n-1)×4=4n-1.
查看更多完整答案,请扫码查看


