第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置。以上这些现象有什么共同特点呢?
(1) 我们可以把上面问题中的指针、叶片等看作平面图形。像这样,把一个平面图形绕着平面内某一点 $ O $ 转动一个角度,叫做图形的
(2) 如果图形上的点 $ P $ 经过旋转变为点 $ P' $,那么这两个点叫做这个旋转的
(3) 由旋转的概念知,旋转改变了图形的什么?没有改变图形的什么?
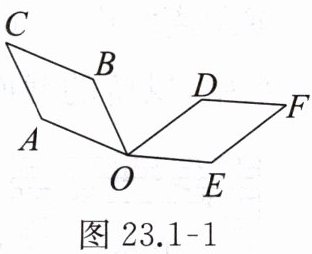
(4) 如图 23.1 - 1,如果把钟表的指针看成四边形 $ AOBC $,它绕着点 $ O $ 顺时针旋转到四边形 $ DOEF $ 的位置,在这个旋转过程中:旋转中心是
(1) 我们可以把上面问题中的指针、叶片等看作平面图形。像这样,把一个平面图形绕着平面内某一点 $ O $ 转动一个角度,叫做图形的
旋转
,点 $ O $ 叫做旋转中心
,转动的角叫做旋转角
。(2) 如果图形上的点 $ P $ 经过旋转变为点 $ P' $,那么这两个点叫做这个旋转的
对应点
。(3) 由旋转的概念知,旋转改变了图形的什么?没有改变图形的什么?
(4) 如图 23.1 - 1,如果把钟表的指针看成四边形 $ AOBC $,它绕着点 $ O $ 顺时针旋转到四边形 $ DOEF $ 的位置,在这个旋转过程中:旋转中心是
点O
,旋转角是∠AOD(或∠BOE)
。经过旋转,点 $ A $ 转到点 $ D $,点 $ C $ 转到点 $ F $,点 $ B $ 转到点 $ E $;线段 $ OA = $OD
,$ OB = $OE
,$ BC = $EF
,$ AC = $DF
;$ \angle A = $∠D
,$ \angle B = $∠E
,$ \angle C = $∠F
。
答案:
(1)旋转 旋转中心 旋转角;
(2)对应点;
(3)旋转改变了图形的位置,没有改变图形的大小、形状;
(4)点O ∠AOD(或∠BOE) OD OE EF DF ∠D ∠E ∠F
(1)旋转 旋转中心 旋转角;
(2)对应点;
(3)旋转改变了图形的位置,没有改变图形的大小、形状;
(4)点O ∠AOD(或∠BOE) OD OE EF DF ∠D ∠E ∠F
旋转的性质
(1) 对应点到旋转中心的距离
(2) 对应点与旋转中心所连线段的夹角等于
(3) 旋转前、后的图形
(1) 对应点到旋转中心的距离
相等
;(2) 对应点与旋转中心所连线段的夹角等于
旋转角
;(3) 旋转前、后的图形
全等
。
答案:
(1)相等;
(2)旋转角;
(3)全等
(1)相等;
(2)旋转角;
(3)全等
1. 下列现象:①钟表上时针的转动;②摩天轮的转动;③地下水位逐年下降;④传送带上的机器人。其中,属于旋转的是(
A.①②
B.②③
C.①④
D.③④
A
)A.①②
B.②③
C.①④
D.③④
答案:
1.A
2. 如图 23.1 - 2 所示,$ \triangle ABC $ 为等边三角形,$ D $ 为 $ BC $ 边上一点,$ \triangle ABD $ 经过旋转后到达 $ \triangle ACP $ 的位置,请回答:
(1) 旋转中心是点
(2) 旋转角的大小是
(3) $ \triangle ADP $ 是

(1) 旋转中心是点
A
;(2) 旋转角的大小是
60°
;(3) $ \triangle ADP $ 是
等边
三角形。
答案:
2.
(1)A;
(2)60°;
(3)等边
(1)A;
(2)60°;
(3)等边
查看更多完整答案,请扫码查看


