《2025年课时练人民教育出版社九年级数学上册人教版》

5. 下列哪些数是方程 $ x^{2}-6x + 8 = 0 $ 的根？
0，1，2，3，4，5，6，7，8，9，10.

答案： 5.解:2,4是方程x²-6x+8=0的根.

1. 下列各选项中是关于 $ x $ 的一元二次方程的是(D)

A.$ x^{2}+\frac{1}{x^{2}}=0 $
B.$ ax^{2}+bx + c = 0 $
C.$ 3x^{2}-2xy - 5y^{2}=0 $
D.$ (x - 1)(x + 2)=1 $

答案： 1.D

2. 一元二次方程 $ x(x - 1)=0 $ 的解是(C)

A.$ x = 0 $
B.$ x = 1 $
C.$ x = 0 $ 或 $ x = 1 $
D.$ x = 0 $ 或 $ x = -1 $

答案： 2.C

3. 方程 $ (x - 1)(x + 3)=12 $ 化为 $ ax^{2}+bx + c = 0 $ 的形式后，$ a $，$ b $，$ c $ 的值分别为(C)

A.1，$ -2 $，$ -15 $
B.$ -1 $，$ -2 $，$ -15 $
C.1，2，$ -15 $
D.$ -1 $，2，$ -15 $

答案： 3.C

4. 若关于 $ x $ 的一元二次方程 $ ax^{2}+bx + 5 = 0 $ 有一个根为 $ x = 1 $，则 $ 214 - a - b = $219.

答案： 4.219

5. 已知 1 是关于 $ x $ 的一元二次方程 $ x^{2}+mx + n = 0 $ 的一个根，求 $ m^{2}+2mn + n^{2} $ 的值.

答案： 5.解:1.

6. 当 $ a $ 为何值时，下列方程是一元二次方程？
(1) $ ax^{2}-x = 2x^{2}-ax - 3 $；
(2) $ (a - 2)x^{a^{2}-2}+3x = 0 $.

答案： 6.解:
(1)当a≠2时,方程ax²-x=2x²-ax-3是一元二次方程.
(2)当a=-2时,原方程是一元二次方程.

7. 关于 $ x $ 的一元二次方程 $ (a - 1)x^{2}+x + a^{2}-1 = 0 $ 的一个根是 0，则 $ a $ 的值为(B)

A.1
B.$ -1 $
C.1 或 $ -1 $
D.$ \frac{1}{2} $

答案： 7.B

8. (安徽中考)一种药品原价每盒 25 元，经过两次降价后每盒 16 元. 设两次降价的百分率都为 $ x $，则 $ x $ 满足(D)

A.$ 16(1 + 2x)=25 $
B.$ 25(1 - 2x)=16 $
C.$ 16(1 + x)^{2}=25 $
D.$ 25(1 - x)^{2}=16 $

答案： 8.D

9. 已知 $ a $，$ b $，$ c $ 为一个三角形三条边的长，求证：$ ax^{2}+bx(x - 1)=cx^{2}-2b $ 是关于 $ x $ 的一元二次方程.

答案： 9.证明:化简ax²+bx(x-1)=cx²-2b,得(a+b-c)x²-bx+2b=0. 因为a,b,c为一个三角形三条边的长,所以a+b＞c, 即a+b-c＞0,所以ax²+bx(x-1)=cx²-2b是关于x的一元二次方程.

10. 某校为提倡学生“多读书，读好书”，每年都要开展“过三关”免费赠书活动. 今年赠书活动的前提是顺利通过设置的三关：在每关内放置一道题，若能在规定的时间内顺利答对三道题，则可免费得到赠书. 同学们，你们想参加吗？快快行动吧！

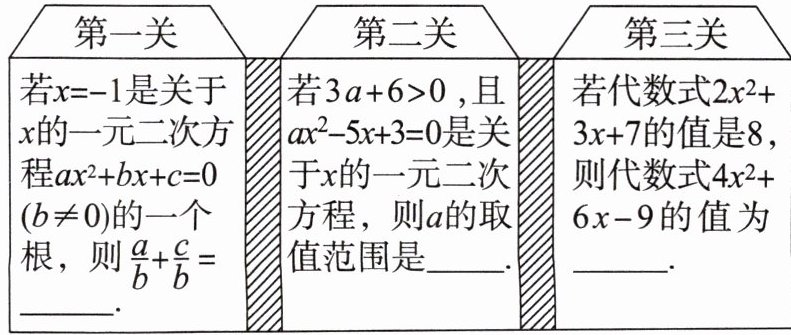
答案： 10.1 a＞-2,且a≠0 -7