《2025年课时练人民教育出版社九年级数学上册人教版》

6. 一个两位数，个位上的数字比十位上的数字小 $4$，且个位上的数字与十位上的数字的平方和比这个两位数小 $4$，设个位上的数字是 $x$，则所列方程为(C)

A.$x^2 + (x + 4)^2=10(x - 4)+x - 4$
B.$x^2 + (x + 4)^2=10x + x + 4$
C.$x^2 + (x + 4)^2=10(x + 4)+x - 4$
D.$x^2 + (x - 4)^2=10x + (x - 4)-4$

答案： 6.C

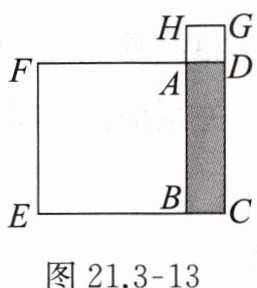
7. 如图 21.3 - 13，矩形 $ABCD$ 的周长是 $20 cm$，分别以 $AB$，$AD$ 为边向外作正方形 $ABEF$ 和正方形 $ADGH$，若正方形 $ABEF$ 和 $ADGH$ 的面积之和为 $68 cm^2$，则矩形 $ABCD$ 的面积是(B)

A.$21 cm^2$
B.$16 cm^2$
C.$24 cm^2$
D.$9 cm^2$
 

答案： 7.B

8. 某商场推销一款新书包，进价为 $30$ 元，在试销中发现这款书包每天的销售量 $P$(单位：个)与每个书包销售价 $x$(单位：元)满足一次函数关系.当定价为 $35$ 元时，每天销售 $30$ 个；当定价为 $37$ 元时，每天销售 $26$ 个.问：要使商场每天销售这款书包获利 $200$ 元，书包的销售单价应定为多少元？

答案： 8.解:要保证商场每天销售这种书包获利200 元,书包的销售单价应定为40 元.

9. 某商店购进 $600$ 个旅游纪念品，进价为 $6$ 元每个.第一周以 $10$ 元每个的价格售出 $200$ 个，第二周若按 $10$ 元每个的价格销售仍可售出 $200$ 个，但商店为了适当增加销量，决定降价销售(根据市场调查，单价每降价 $1$ 元，可多售出 $50$ 个，但售价不得低于进价).单价降低 $x$ 元销售一周后，商店对剩余旅游纪念品清仓处理，以 $4$ 元每个的价格全部售出.如果该商店销售这批旅游纪念品共获利 $1250$ 元，问：第二周每个旅游纪念品的销售价格为多少元？

答案： 9.解:第二周每个旅游纪念品的销售价格为9 元.

10. 如图 21.3 - 14，已知在 $\triangle ABC$ 中，$\angle B = 90°$，$AB = 5 cm$，$BC = 7 cm$，点 $P$ 从点 $A$ 开始沿边 $AB$ 向点 $B$ 以 $1 cm/s$ 的速度移动，点 $Q$ 从点 $B$ 开始沿边 $BC$ 向点 $C$ 以 $2 cm/s$ 的速度移动.
(1) 如果 $P$，$Q$ 分别从 $A$，$B$ 同时出发，那么几秒后，$\triangle PBQ$ 的面积等于 $4 cm^2$？
(2) 如果 $P$，$Q$ 分别从 $A$，$B$ 同时出发，那么几秒后，$PQ$ 的长度等于 $5 cm$？
(3) 如果 $P$，$Q$ 分别从 $A$，$B$ 同时出发，$\triangle PQB$ 的面积能否等于 $7 cm^2$？请说明理由.
[img]
图 21.3 - 14

答案： 1. （1）
设$t$秒后，$\triangle PBQ$的面积等于$4cm^{2}$。
已知$AP = tcm$，$BQ = 2tcm$，则$PB=(5 - t)cm$。
根据三角形面积公式$S=\frac{1}{2}ah$（这里$a = PB$，$h = BQ$），可得$S_{\triangle PBQ}=\frac{1}{2}(5 - t)×2t$。
因为$S_{\triangle PBQ}=4$，所以$\frac{1}{2}(5 - t)×2t = 4$。
化简得$5t-t^{2}=4$，即$t^{2}-5t + 4 = 0$。
因式分解$(t - 1)(t - 4)=0$。
解得$t_{1}=1$，$t_{2}=4$。
当$t = 4$时，$BQ=2t = 8\gt7$，不符合题意，舍去。
所以$1$秒后，$\triangle PBQ$的面积等于$4cm^{2}$。
2. （2）
设$x$秒后，$PQ$的长度等于$5cm$。
由$AP = xcm$，$BQ = 2xcm$，则$PB=(5 - x)cm$。
根据勾股定理$PQ^{2}=PB^{2}+BQ^{2}$，已知$PQ = 5$，所以$(5 - x)^{2}+(2x)^{2}=25$。
展开得$25-10x+x^{2}+4x^{2}=25$。
合并同类项$5x^{2}-10x = 0$，提取公因式$5x(x - 2)=0$。
解得$x_{1}=0$（舍去），$x_{2}=2$。
所以$2$秒后，$PQ$的长度等于$5cm$。
3. （3）
设$y$秒后，$\triangle PQB$的面积等于$7cm^{2}$。
由$AP = ycm$，$BQ = 2ycm$，则$PB=(5 - y)cm$。
根据三角形面积公式$S_{\triangle PQB}=\frac{1}{2}(5 - y)×2y$。
若$S_{\triangle PQB}=7$，则$\frac{1}{2}(5 - y)×2y = 7$。
化简得$5y-y^{2}=7$，即$y^{2}-5y + 7 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a = 1,b=-5,c = 7)$，其判别式$\Delta=b^{2}-4ac=(-5)^{2}-4×1×7=25 - 28=-3\lt0$。
所以方程$y^{2}-5y + 7 = 0$无实数根。
所以$\triangle PQB$的面积不能等于$7cm^{2}$。
综上，答案依次为：（1）$1$秒；（2）$2$秒；（3）不能，理由见上述步骤。