《2025年一遍过八年级数学上册苏科版》

1 [2024南通金北学校段考]下列式子中,表示y是x的正比例函数的是 (C)
A.$y = x^{2}$
B.$y = \frac{2}{x}$
C.$y = \frac{x}{3}$
D.$y^{2} = 3x$

答案： C 在$y=x^{2}$中,自变量的次数为2,选项A不是正比例函数;在$y=\frac {2}{x}$中,自变量的次数为-1,选项B不是正比例函数;在$y=\frac {x}{3}$中,自变量的次数为1,选项C是正比例函数;在$y^{2}=3x$中,自变量的次数为1,但变量y的次数是2,选项D不是正比例函数.

下列函数关系中,属于正比例函数关系的是 (D)
A.圆的面积S与它的半径r
B.面积是常数S时,长方形的长y与宽x
C.路程是常数s时,行驶的速度v与时间t
D.三角形的底边是常数a时,它的面积S与这条边上的高h

答案： D 选项A中,$S=πr^{2}$,S与r不是正比例函数关系;选项B中,$y=\frac {S}{x}$,y与x不是正比例函数关系;选项C中,$v=\frac {s}{t}$,v与t不是正比例函数关系;选项D中,$S=\frac {1}{2}ah$(a为常数),S与h是正比例函数关系.

3 [2025苏州立达中学月考]若$y = kx + 2k + x$是关于x的正比例函数,则k的值为0.

答案： 0 $y=kx+2k+x=(k+1)x+2k$.$\because y=kx+2k+x$是关于x的正比例函数,$\therefore k+1≠0$且$2k=0$,解得$k=0$.

函数①$y = kx + b$;②$y = 2x$;③$y = -\frac{3}{x}$;④$y = \frac{1}{3}x + 3$;⑤$y = x^{2} - 2x + 1$中,一次函数有 (B)
A.1个
B.2个
C.3个
D.4个

答案： B ①$y=kx+b$,当$k=0$时,不是一次函数;②$y=2x$是一次函数;③$y=-\frac {3}{x}$不是一次函数;④$y=\frac {1}{3}x+3$是一次函数;⑤$y=x^{2}-2x+1$不是一次函数.一次函数共有2个.

在一次函数$y = -2x - 1$中,当$x = -5$时,$y = $9;当$y = -7$时,$x = $3.

答案： 9 3 把x,y的值分别代入一次函数表达式$y=-2x-1$中.当$x=-5$时,$y=-2×(-5)-1=9$;当$y=-7$时,$-7=-2x-1$,解得$x=3$.

6 [2025盐城射阳县实验初中月考]已知函数$y = (m - 2)x^{3 - |m|} + m + 7$.
(1)当m为何值时,y是x的一次函数?
(2)若该函数是一次函数,则x为何值时,y的值为3?

答案： 解:
(1)由题意,得$\left\{\begin{array}{l} 3-|m|=1,\\ m-2≠0,\end{array}\right. $解得$m=-2$.
∴当$m=-2$时,y是x的一次函数.
(2)$\because m=-2$,
∴一次函数表达式为$y=-4x+5$.当$y=3$时,$3=-4x+5$,解得$x=\frac {1}{2}$.
∴当$x=\frac {1}{2}$时,y的值为3.

7 油箱中有油20升,油从管道中匀速流出,100分钟流完.油箱中剩油量Q(升)与流出的时间t(分)之间的函数表达式是 (C)
A.$Q = 20 - 5t$
B.$Q = \frac{1}{5}t + 20$
C.$Q = 20 - \frac{1}{5}t$
D.$Q = \frac{1}{5}t$

答案： C
∵100分钟可流完20升油,
∴1分钟可流油$20÷100=\frac {1}{5}$(升),
∴t分钟流的油量为$\frac {1}{5}t$升,$\therefore Q=20-\frac {1}{5}t$.

8 一个正方形的边长为3cm,它的各边长减少xcm($0 ＜ x ＜ 3$)后,得到的新正方形的周长为ycm,则y与x之间的函数表达式是$y=12-4x$.

答案： $y=12-4x$

9 [2024南通启东期末]图1是一个轴对称图形,且每个角都是直角,长度如图1所示.小明用x个这样的图形,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙,则图形的总长度y与图形个数x之间的函数表达式为____.


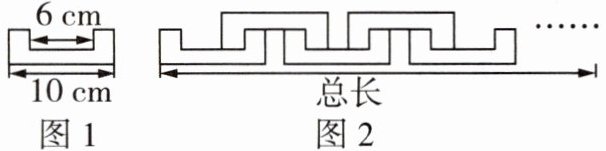
$y=6x+4$

答案： $y=6x+4$ 由题图2,得$y=10+6(x-1)$,$\therefore y=6x+4$.

10 [2025苏州星湖学校期中]某市出租车的收费标准如下:起步价5元,即3千米以内(含3千米)收费5元,超过3千米的部分,每千米收费2元.求车费y(元)与行程x(千米)之间的函数表达式.

答案： 解:根据题意可知,当$0＜x≤3$时,$y=5$,当$x＞3$时,$y=5+2(x-3)=2x-1$,$\therefore y=\left\{\begin{array}{l} 5(0＜x≤3),\\ 2x-1(x＞3).\end{array}\right. $